题目内容
【题目】以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则该三角形的面积是（ ）
A.
B.
C.
D.
【答案】D
【解析】解：如图1，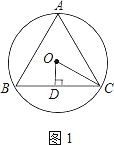
∵OC=1，
∴OD=1×sin30°= 
；
如图2，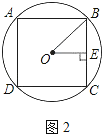
∵OB=1，
∴OE=1×sin45°= 
；
如图3，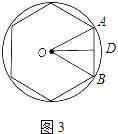
∵OA=1，
∴OD=1×cos30°= 
，则该三角形的三边分别为： 
、 、 ，∵（ ）2+（ ）2=（ ）2 ， ∴该三角形是以 
、 
为直角边， 
为斜边的直角三角形，∴该三角形的面积是 × × = 
，
故选：D．
由于内接正三角形、正方形、正六边形是特殊内角的多边形，可构造直角三角形分别求出边心距的长，由勾股定理逆定理可得该三角形是直角三角形，进而可得其面积．本题主要考查多边形与圆，解答此题要明确：多边形的半径、边心距、中心角等概念，根据解直角三角形的知识解答是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某市团委举办“我的中国梦”为主题的知识竞赛，甲、乙两所学校参赛人数相等，比赛结束后，发现学生成绩分别为70分、80分、90分、100分，并根据统计数据绘制了如下不完整的统计图表：
乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中，“80分”所在扇形的圆心角度数为________；
(2)请你将图②补充完整；
(3)求乙校成绩的平均分；
(4)经计算知s甲2＝135，s乙2＝175，请你根据这两个数据，对甲、乙两校成绩作出合理评价．
