题目内容
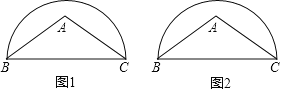
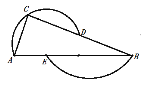
【题目】过A,C,D三点的圆的圆心为E,过B,E两点的圆的圆心为D,如果∠A=60°,那么∠B为________.
【答案】20°
【解析】
连接DE、CE,如图,设∠B=x,根据等腰三角形的性质由EA=EC得到∠A=∠ACE,再根据三角形内角和定理得到∠4=180°-2∠A=180°-120°=60°,而DE=DB,∠1=∠B=x,利用三角形外角性质得到∠2=∠1+∠B=2x,然后根据三角形外角性质得到2x+x=60°,即可解答.
连接DE、CE,如图,设∠B=x

∵过A,C,D三点的圆的圆心为E,
∴EA=EC=ED
∴∠A=∠ACE
∴∠4=180°-2∠A=180°-120°=60°
∵过B,E两点的圆的圆心为D,
∴DE=DB
∴∠1=∠B=x
∴∠2=∠1+∠B=2x
而EC=ED
∴∠3=∠2=2x
∵4=∠3+∠B
∴2x+x=60°,即x=20°
即∠B=20°
故答案为:20°

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目