题目内容
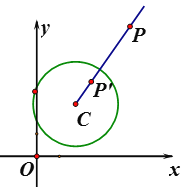
【题目】 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为奇妙四边形.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据奇妙四边形对角线互相垂直的特征可得奇妙四边形的一个重要性质:奇妙四边形的面积等于两条对角线乘积的一半.根据以上信息回答:

(1)矩形 奇妙四边形(填“是”或“不是”);
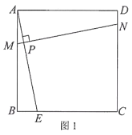
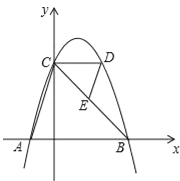
(2)如图2,已知⊙O的内接四边形ABCD是奇妙四边形,若⊙O的半径为6,∠ BCD=60°.求奇妙四边形ABCD的面积;
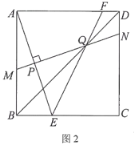
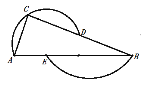
(3)如图3,已知⊙O的内接四边形ABCD是奇妙四边形作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.
【答案】(1)不是;
(2)54;
(3)![]() .
.
【解析】
(1)根据矩形的性质和“奇妙四边形”的定义进行判断;
(2)连结OB、OD,作OH⊥BD于H,如图2,根据垂径定理,得到BH=DH,根据圆周角定理得到∠BOD=2∠BCD=120°,则利用等腰三角形的性质得∠OBD=30°,在Rt△OBH中可计算出![]() ,
,![]() ,则
,则![]() ,然后根据奇妙四边形”的面积等于两条对角线乘积的一半求解;
,然后根据奇妙四边形”的面积等于两条对角线乘积的一半求解;
(3)连结OB、OC、OA、OD,作OE⊥AD于E,如图3,根据垂径定理得到AE=DE,再利用圆周角定理得到∠BOM=∠BAC,∠AOE=∠ABD,再利用等角的余角相等得到∠OBM=∠AOE,则可证明△BOM≌△OAE得到OM=AE,于是有![]() .
.
解:(1)矩形的对角线相等但不垂直,
所以矩形不是奇妙四边形;
故答案为:不是;
(2)

连结OB、OD,作OH⊥BD于H,如图2,则BH=DH,
∵∠BOD=2∠BCD=2×60°=120°,
∴在等腰△OBD中,∠OBD=30°,
在Rt△OBH中,∵∠OBH=30°,
∴![]() ,
,
∴![]()
∴![]()
∵四边形ABCD是奇妙四边形,
∴![]() ,
,![]()
∴![]() ;
;
(3)![]() .
.
理由如下: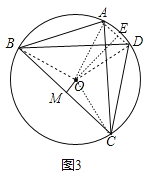
连结OB、OC、OA、OD,作OE⊥AD于E,如图3,
∵OE⊥AD,
∴在等腰△AOD中,![]() ,
,
又∵![]() ,
,
∴∠BOM=∠BAC,
同理可得∠AOE=∠ABD,
∵BD⊥AC,
∴∠BAC+∠ABD=90°,
∴∠BOM+∠AOE=90°,
∵∠BOM+∠OBM=90°,
∴∠OBM=∠/span>AOE,
在△BOM和△OAE中

∴![]() ,
,
∴OM=AE,
∴![]() .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题:
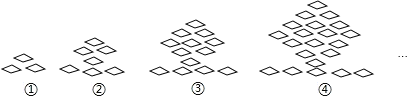
(1)填写下表:
图形序号 | 菱形个数 |
| 3 |
| 7 |
| ______ |
| ______ |
|
|
(2)根据表中规律猜想,图n中菱形的个数![]() 用含n的式子表示,不用说理
用含n的式子表示,不用说理![]() ;
;
(3)是否存在一个图形恰好由91个菱形组成?若存在,求出图形的序号;若不存在,说明理由.