题目内容
【题目】如图,点![]() 是
是![]() 的边
的边![]() 的延长线上一点,点
的延长线上一点,点![]() 是边
是边![]() 上的一点(不与点
上的一点(不与点![]() 重合).以
重合).以![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,又
,又![]() (点
(点![]() 、
、![]() 在直线
在直线![]() 的同侧),如果
的同侧),如果![]() ,那么
,那么![]() 的面积与
的面积与![]() 面积的比值为____________.
面积的比值为____________.
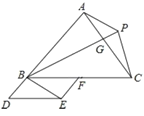
【答案】3:4
【解析】
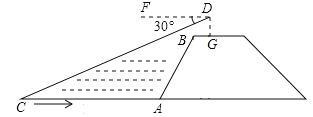
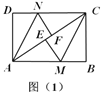
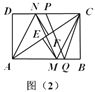
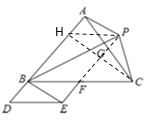
首先过点P作PH//BC交AB于H,连接CH,PF,易得四边形APEB、BFPH是平行四边形,又由四边形BDEF是平行四边形,设BD=a,则AB=4a,可求得BH=PF=3a,又由S△HBC=S△PBC,S△HBC:S△ABC=BH::AB,即可求得△PBC的面积与△ABC面积之比.
过点P作PH//BC交AB于H,连接CH,PF,
∵AP∥BE,AP=BE,
∴四边形APEB是平行四边形,
∴PE∥AB,PE=AB,
∵四边形BDEF是平行四边形,
∴EF∥BD,EF=BD,
∴EF∥AB,
∴P、E、F共线,
设BD=a,
∵![]() ,
,
∴PE=AB=4a,
则PF=PE-EF=3a,
∵PH∥BC,
∴S△HBC=S△PBC,
∵PF∥AB,
∴易得四边形BFPH是平行四边形,
∴BH=PF=3a,
∵S△HBC:S△ABC=BH::AB=3a:4a=3:4,
∴![]() 的面积与
的面积与![]() 面积的比值为3:4,
面积的比值为3:4,
故答案为:3:4.

练习册系列答案
相关题目