题目内容
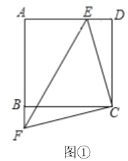
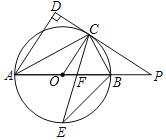
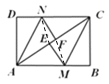
【题目】如图(1),在矩形![]() 中,把
中,把![]() 、
、![]() 分别翻折,使点
分别翻折,使点![]() 、
、![]() 分别落在对角线
分别落在对角线![]() 上的点
上的点![]() 、
、![]() 处,折痕分别为
处,折痕分别为![]() 、
、![]() .
.
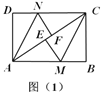
(1)求证:![]() .
.
(2)请连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 是平行四边形
是平行四边形
(3)![]() 、
、![]() 是矩形的边
是矩形的边![]() 、
、![]() 上的两点,连结
上的两点,连结![]() 、
、![]() 、
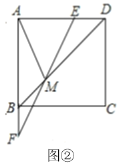
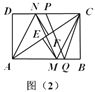
、![]() ,如图(2)所示,若
,如图(2)所示,若![]() ,
,![]() .且
.且![]() ,
,![]() ,求
,求![]() 的长度.
的长度.
【答案】(1)见解析;(2)见解析;(3)PC=2
【解析】
(1)根据折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,从而根据AD∥BC可得出∠DAN=∠BCM,从而即可判断出△ADN≌△CBM;
(2)连接NE、MF,根据(1)的结论可得出NF=ME,再由∠NFE=∠MEF可判断出NF∥ME,即可得到结论;
(3)设AC与MN的交点为O,EF=x,作QG⊥PC于G点,首先求出AC=5,根据翻折变换知:AF=CE=3,于是可得AF+(CE-EF)=5,可得EF=1,在Rt△NFE中,NO2=NF2+OF2,求出NO的长,即NM=PQ=QC=2NO,PC=2![]() .
.
(1)证明:∵四边形ABCD是正方形,
∴AD=BC,∠B=∠D=90°,
由折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,
∵AD//BC,
∴∠DAC=∠BCA,
∴∠DAN=∠BCM,
在Rt△AND和Rt△CMB中,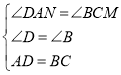 ,
,
∴△AND≌△CMB(AAS)
(2)由(1)得:△AND≌△CMB,
∴NF=ME,
∵∠NFE=∠MEF,.
∴NF∥ME,
∴四边形MFNE是平行四边形;
(3)设AC与MN的交点为O,EF=x,作QG⊥PC于G,如图所示:
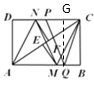
∵AB=4,BC=3,
∴AC=5,
∵AF=CE=BC=3,
∴2AF-EF=AC,即6-x=5,
解得x=1,
∴EF=1,
∴CF=2,
由折叠的性质得:NF=DN=![]() ,
,
∵OE=OF=![]() EF=
EF=![]() ,
,
∴在Rt△NFO中,ON2=OF2+NF2,
∴ON=![]() ,
,
∴MN=2ON=![]() ,
,
∵PQ∥MN,PN∥MQ,
∴四边形MQPN是平行四边形,
∴MN=PQ=![]() ,
,
∵PQ=CQ,
∴△PQC是等腰三角形,
∴PG=CG,
在Rt△QPG中,PG2=PQ2-QG2,
∴PG=![]() =1,
=1,
∴PC=2PG=2.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案【题目】我们知道“距离地面越高,温度越低”,下表给出了距离地面的高度与所在位置的温度之间的大致关系.
距离地面的高度(千米) | 0 | 1 | 2 | 3 | 4 | 5 |
所在位置的温度(C) | 20 | 14 | 8 | 2 |
|
|
(1)上表中哪个是自变量?
(2)由表可知,距离地面高度每上升1千米,温度降低______℃;
(3)2018年5月14日,四川航空3U8633航班执行重庆—拉萨航班任务,飞行途中,在距离地面9800米的高空,驾驶舱右侧挡风玻璃突然破裂,2名飞行员在超低压、超低温的紧急情况下,冷静应对,最终飞机成功降落,创造了世界航空史上的奇迹,请你计算出飞机发生事故时所在高空的温度(假设当时所在位置的地面温度为20℃).