题目内容
如图,直角梯形OABC中,OC∥AB,C(0,3),B(4,1),以BC为直径的圆交x轴于D、E两点(点D在点E的右方)求点E、D的坐标.


D(3,0),E(1,0)
解:∵BC是直径,∴∠BDC=90°,

∴∠1+∠2=90°,
又∵∠1+∠3=90°,
∴∠2=∠3,
在△ODC和△ABD中,
∠COD=∠DAB=90°,
∠2=∠3,∴△ODC∽△ABD,
∴
 =
= ,
,又∵AB=1,OC=3,∴
 =
= .∴OD·AD=3,
.∴OD·AD=3,又∵OD+AD=4,∴AD=4-OD,
设OD=x则x(4-x)=3,解得x1=1,x2=3,
即以BC为直径的圆与x轴有两个交点,它们在原点的右侧,与原点的距离分别为1和3,由于点D在点E的右侧,∴OE=1,OD=3,所以点D、E的坐标分别为D(3,0),E(1,0).

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目

 ,
, ,则点A′的坐标 .
,则点A′的坐标 .
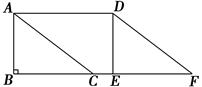
 是正方形,延长
是正方形,延长 到
到 ,使
,使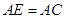 ,则
,则 的度数是 °
的度数是 °

