题目内容
【题目】如图,在平面直角坐标系中,直线y=﹣x+8分别交两轴于点A、B,点C的横坐标为4,点D在线段OA上,且AD=7.
(1)求直线CD的解析式;
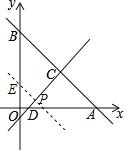
(2)P为直线CD上一点,若△PAB面积为20,求P的坐标;
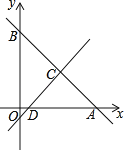
【答案】(1)y=![]() ;(2)P(
;(2)P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() ).
).
【解析】
(1)首先根据直线y=-x+8分别交两轴于点A、B,可得点A的坐标是(8,0),点B的坐标是(0,8);然后根据点C为线段AB的中点,可得点C的坐标是(4,4);根据AD的长,即可求出点D的坐标,然后利用待定系数法可求直线CD的解析式;
(2)求得AB边上的高,即可求得过P点且与直线AB平行的直线与y轴的交点E的坐标,即可求得此直线的解析式,然后与直线CD联立,解方程组即可求得.
(1)∵直线y=-x+8分别交两轴于点A、B,
∴当x=0时,y=8,当y=0时,x=8
∴点A(8,0),点B(0,8)
∵点D在线段OA上,且AD=7.
∴点D(1,0)
∵点C的横坐标为4,且在直线y=-x+8上,
∴y=-4+8=4
∴点C(4,4)
设直线CD的解析式y=kx+b
∴![]() ,
,
解得:k=![]() ,b=-
,b=-![]() ,
,
∴直线CD解析式为:y=![]() x
x![]() ;
;
(2)∵点A(8,0),点B(0,8),
∴OA=OB,AB=8![]() ,
,
∴∠ABO=45°,
∵△PAB面积为20,
∴AB边上的高为![]() ,
,
设过P点且与直线AB平行的直线交y轴于E,则BE=5
∴E(0,3)或(0,13),
∴过P点且平行与直线AB的直线为y=-x+3或y=-x+13,
解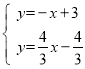 得
得![]() ,
,
解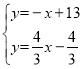 得
得 ,
,
故P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() ).
).

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目




