题目内容
【题目】如图,已知l1∥l2,MN分别和直线l1、l2交于点A、B,ME分别和直线l1、l2交于点C、D,点P在MN上(P点与A、B、M三点不重合).
(1)如果点P在A、B两点之间运动时,∠α、∠β、∠γ之间有何数量关系请说明理由;
(2)如果点P在A、B两点外侧运动时,∠α、∠β、∠γ有何数量关系(只须写出结论).

【答案】(1)∠α+∠β=∠γ.(2)①P在A点左边时,∠α﹣∠β=∠γ;②P在B点右边时,∠β﹣∠α=∠γ.
【解析】分析:(1)根据平行线的性质可求出它们的关系,从点P作平行线,平行于AC,根据两直线平行内错角相等可得出.
(2)分类讨论,①点P在点A左边,②点P在点B右边.
详解:(1)如图,过点P做AC的平行线PO,
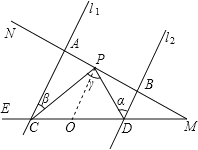
∵AC∥PO,
∴∠β=∠CPO,
又∵AC∥BD,
∴PO∥BD,
∴∠α=∠DPO,
∴∠α+∠β=∠γ.
(2)①P在A点左边时,∠α∠β=∠γ;
②P在B点右边时,∠β∠α=∠γ.
(提示:两小题都过P作AC的平行线).

练习册系列答案
相关题目