题目内容
【题目】如图,在Rt△ABC中,∠C=90°,P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为Q,连接AP.若AC=3,BC=4,则△AQP的面积的最大值是( ) 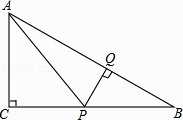
A.![]()
B.![]()
C.![]()
D.![]()
【答案】C
【解析】解:设BP=x(0<x<4),由勾股定理得 AB=5, ∵∠PQB=∠C=90°,∠B=∠B,
∴△PBQ∽△ABC,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]()
∴PQ= ![]() x,QB=
x,QB= ![]() x
x
S△APQ= ![]() PQ×AQ=
PQ×AQ= ![]() +
+ ![]() x=
x= ![]()
∴当x= ![]() 时,△APQ的面积最大,最大值是
时,△APQ的面积最大,最大值是 ![]() .
.
故选(C)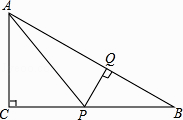
【考点精析】通过灵活运用二次函数的最值和相似三角形的判定与性质,掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目