题目内容
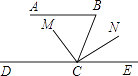
【题目】如图,△ABC中,点D、E分别在AB、AC上,△ABE≌△ACD.
(1)求证:△BEC≌△CDB;
(2)若∠A=70°,BE⊥AC,求∠BCD的度数.

【答案】见解析
【解析】试题分析:(1)利用△ABE≌△ACD,得BE=CD,BD=CE,一条公共边,BC=BC,利用SSS证明.
(2)利用(1)结论,可知∠ACD=∠ABE=20°,由内角和180°,可知∠EBC+∠DCB=70°,可得∠BCD的度数.
试题解析:
(1)证明:∵△ABE≌△ACD,
∴AB=AC,AD=AE,BE=CD,
∴BD=CE,
在△BEC与△CDB中,
BD=CE,CD=BE,BC=CB,
∴△BEC≌△CDB.
(2)解:∵AB=AC,∠A=70°,
∴∠ACB=∠ABC=55°,
∵BE⊥AC,
∴∠BEC=∠AEB=90°,
∴∠ABE=∠ACD=20°,
∴∠BCD=35°.

练习册系列答案
相关题目