题目内容
【题目】已知动点P以每秒2cm的速度沿图甲的边框按BCDEFA的路径移动，相应的三角形ABP的面积S（cm2）与时间t（秒）之间的关系用图乙中的图象表示，若AB=6cm，试回答下列问题：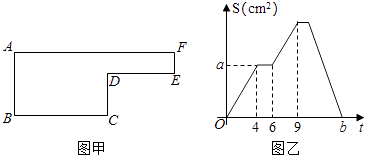
（1）图甲中的BC长是多少？
（2）图乙中的a是多少？
【答案】
（1）
解：动点P在BC上运动时，对应的时间为0到4秒，易得：BC=2cm/秒×4秒=8cm；
故图甲中的BC长是8cm
（2）
解：由（1）可得，BC=8cm，则：a= 
×BC×AB=24cm2；
图乙中的a是24cm2
【解析】（1）根据题意得：动点P在BC上运动的时间是4秒，又由动点的速度，可得BC的长；（2）由（1）可得BC的长，又由AB=6cm，可以计算出△ABP的面积，计算可得a的值．
【考点精析】本题主要考查了函数的图象的相关知识点，需要掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值才能正确解答此题．
练习册系列答案
相关题目
