题目内容
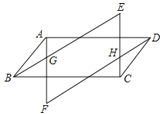
【题目】如图，四边形ABCD是平行四边形，作AF∥CE，BE∥DF，AF交BE与G点，交DF与F点，CE交DF于H点、交BE于E点．求证：△EBC≌△FDA．
【答案】证明过程见解析
【解析】
试题分析：根据平行四边形的性质得到AD和BC平行且相等，根据AF∥CE，BE∥DF得出四边形四边形GFHE和四边形AMCN是平行四边形，则∠FAD=∠ECB，∠ADF=∠EBC，从而说明三角形EBC和△FDA全等.
试题解析：∵四边形ABCD是平行四边形，∴AD=BC，AD∥BC，∵AF∥CE，BE∥DF，
∴四边形GFHE和四边形AMCN是平行四边形， ∴∠FAD=∠ECB，∠ADF=∠EBC，
在△EBC和△FDA中，
∴△EBC≌△FDA．
练习册系列答案
天天向上口算本系列答案
相关题目
