Question

【题目】如图，△ABC中，∠ACB＝90°，AC＝4，BC＝3，点P是AB边上一动点．

当△PCB是等腰三角形时，求AP的长度.

Answer 1

【答案】AP的长为2.5或2或1.4.

【解析】试题分析：

当△PCB为等腰三角形时，存在3种情况：①PC＝PB、②BC＝BP、③CB＝CP，结合已知条件分上面三种情况讨论解出对应的AP长度即可.

试题解析：

∵在△ABC中，∠ACB＝90°，AC＝4，BC＝3，

∴AB＝=5.

当△PCB为等腰三角形时，存在3种情况：①PC＝PB、②BC＝BP、③CB＝CP，现分别讨论如下：

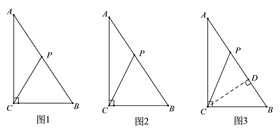
① 如图1，在△ABC中，∵∠ACB＝90°，

∴当点P是AB的中点时，PC＝PB=AP=AB，△PCB是等腰三角形，此时：AP＝AB =2.5；

② 如图2，当BP=BC=3时，△PCB是等腰三角形，此时AP＝AB-BC=5-3=2；

③ 如图3，当CB＝CP时，△PCB是等腰三角形，此时过点C作CD⊥AB于点D，则DP＝DB，

∵在△ABC中， ，

∴，解得CD=2.4.

∴在Rt△CBD中，利用勾股定理可得：BD＝=1.8.

∴ BP＝2BD＝3.6.

∴ AP＝AB-BP=1.4.

综上上述：若△PCB是等腰三角形，则AP的长为2.5或2或1.4.