题目内容
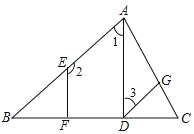
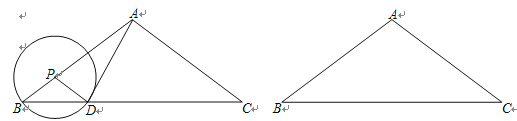
【题目】如图,已知在△ABC中,AB=AC=5,cosB=![]() ,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
,P是边AB上一点,以P为圆心,PB为半径的⊙P与边BC的另一个交点为D,联结PD、AD.
(1)求△ABC的面积;
(2)设PB=x,△APD的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△APD是直角三角形,求PB的长.
【答案】(1)12(2)y= ![]() (0<x<5)(3)
(0<x<5)(3)![]() 或
或![]()
【解析】试题分析:(1)过点A作AH⊥BC于点H ,根据cosB=![]() 求得BH的长,从而根据已知可求得AH的长,BC的长,再利用三角形的面积公式即可得;
求得BH的长,从而根据已知可求得AH的长,BC的长,再利用三角形的面积公式即可得;
(2)先证明△BPD∽△BAC,得到![]() =
=![]() ,再根据
,再根据![]() ,代入相关的量即可得;
,代入相关的量即可得;
(3)分情况进行讨论即可得.
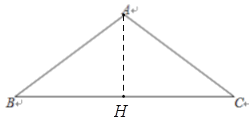
试题解析:(1)过点A作AH⊥BC于点H ,则∠AHB=90°,∴cosB=![]() ,
,
∵cosB=![]() ,AB=5,∴BH=4,∴AH=3,
,AB=5,∴BH=4,∴AH=3,
∵AB=AC,∴BC=2BH=8,
∴S△ABC=![]() ×8×3=12
×8×3=12
(2)∵PB=PD,∴∠B=∠PDB,
∵AB=AC,∴∠B=∠C,∴∠C=∠PDB,
∴△BPD∽△BAC,
∴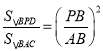 ,
,
即![]() ,
,
解得![]() =
=![]() ,
,
∴![]() ,
,
∴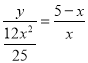 ,
,
解得y= ![]() (0<x<5);
(0<x<5);
(3)∠APD<90°,
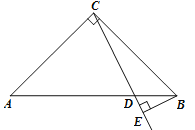
过C作CE⊥AB交BA延长线于E,可得cos∠CAE=![]() ,
,
①当∠ADP=90°时,
cos∠APD=cos∠CAE=![]() ,
,
即![]() ,
,
解得x=![]() ;
;
②当∠PAD=90°时,
![]() ,
,
解得x=![]() ,
,
综上所述,PB=![]() 或
或![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】国家实行一系列“三农”优惠政策后,农民收入大幅度增加.某乡所辖村庄去年的年人均收入(单位:元)情况如下表:
年人均收入 | 3 500 | 3 700 | 3 800 | 3 900 | 4 500 |
村庄个数 | 1 | 1 | 3 | 3 | 1 |
该乡去年各村庄年人均收入的中位数是( )
A.3 700元B.3 800元C.3 850元D.3 900元