Question

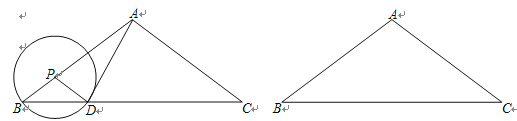
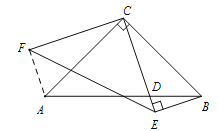
【题目】如图，已知Rt△ABC中，∠ACB=90°，AC=BC，D是线段AB上的一点（不与A、B重合）．过点B作BE⊥CD，垂足为E．将线段CE绕点C顺时针旋转，得到线段CF，连结EF．设∠BCE度数为.

（1）①补全图形；

②试用含的代数式表示∠CDA．

（2）若 ，求的大小．

（3）直接写出线段AB、BE、CF之间的数量关系．

Answer 1

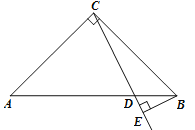
【答案】（1）①答案见解析；②；（2）；（3）．

【解析】试题分析：（1）①按要求作图即可；

②由∠ACB=90°，AC=BC，得∠ABC=45°,故可得出结论；

（2）易证∽，得；连结FA，得△AFC是直角三角形，求出∠ACF=30°，从而得出结论；

（3）.

试题解析：（1）①补全图形．

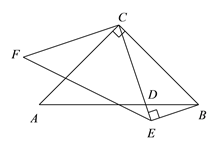
②∵∠ACB=90°，AC=BC，

∴∠ABC=45°

∵∠BCE=

∴∠CDA=

（2）在和中， ，

∽

连结FA．

=

在Rt中， ，

即.

（3）