题目内容
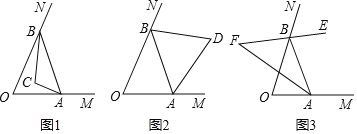
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
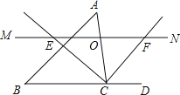
(1)求证:OE=OF;
(2)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?
【答案】(1)证明见解析,(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形.证明见解析,(3)当点O在边AC上运动到AC中点时,若∠ACB=90°,四边形AECF为正方形.证明见解析.
【解析】
(1)根据平行线的性质以及角平分线的性质得出∠1=∠2,∠3=∠4,进而得出答案;
(2)根据AO=CO,EO=FO可得四边形AECF平行四边形,再证明∠ECF=90°利用矩形的判定得出即可;
(3)当点O在边AC上运动到AC中点时,若∠ACB=90°,四边形AECF为正方形,首先证明为矩形,再证明AC⊥EF根据对角线互相垂直的矩形是正方形可得结论.
(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;

(2)当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:如图,当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
![]() 分别平分
分别平分![]()
![]() ∠ECF=90°,
∠ECF=90°,
∴平行四边形AECF是矩形.

(3)当点O在边AC上运动到AC中点时,若∠ACB=90°,四边形AECF为正方形.
证明:如图,由(2)可得点O在边AC上运动到AC中点时平行四边形AECF是矩形,
∵∠ACB=90°,
∴∠2=45°,
∵平行四边形AECF是矩形,
∴EO=CO,
∴∠1=∠2=45°,
∴∠MOC=90°,
∴AC⊥EF,
∴四边形AECF是正方形.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案