题目内容
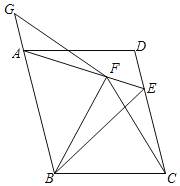
【题目】在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.
(1)若CD=6,AF=3,求△ABF的面积;
(2)求证:BE=AG+CE.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)根据△ABE为等边三角形,就可以求出△ABE在边AE上的高,因此就可以计算出S△ABF;
(2)首先作FH⊥AB于H,CJ⊥AE交AE的延长线于J,再证明△ABF≌△EBC(SAS),同时证明△FHA≌△CJE(AAS),从而证明Rt△FGH≌Rt△CJF(HL),因此可以得到EF=AG,进而证明BE=AE=AF+EF。
(1)解:∵△ABE是等边三角形,
∴∠BAF=60°,AB=AE,
∵四边形ABCD是平行四边形,
∴AB=CD=6,
∴AE=AB=6,
∵AF=3,
∴AF=EF,
∴S△ABF=![]() S△ABE=
S△ABE=![]()
![]() 62=
62=![]() .
.
(2)作FH⊥AB于H,CJ⊥AE交AE的延长线于J.
∵△ABE,△FBC都是等边三角形,
∴BA=BE,BF=BC,∠ABE=∠FBC=60°,
∴∠ABF=∠EBC,
∴△ABF≌△EBC(SAS),
∴AF=EC,
∵AB∥CD,
∴∠CEJ=∠FAH,
∵∠FHA=∠J=90°,
∴△FHA≌△CJE(AAS),
∴FH=CJ,AH=EJ,
∵FB=FG=FC,FH=CJ,
∴Rt△FGH≌Rt△CJF(HL),
∴GH=FJ,∵AH=EJ,
∴EF=AG,
∵BE=AE=AF+EF,
∴BE=RC+AG.


练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目