题目内容
【题目】我们知道,(k+1)2=k2+2k+1,变形得:(k+1)2﹣k2=2k+1,对上面的等式,依次令k=1,2,3,…得:
第1个等式:22﹣12=2×1+1
第2个等式:32﹣22=2×2+1
第3个等式:42﹣32=2×3+1
(1)按规律,写出第n个等式(用含n的等式表示):第n个等式 .
(2)记S1=1+2+3+…+n,将这n个等式两边分别相加,你能求出S1的公式吗?
【答案】(1)(n+1)2﹣n2=2n+1;(2)![]() .
.
【解析】
(1)根据已知算式得出的结果得出规律,即可得出答案;
(2)根据已知得出算式,再相加,即可得出答案.
解:(1)(n+1)2﹣n2=2n+1,
故答案为:(n+1)2﹣n2=2n+1;
(2)∵22﹣12=2×1+1①,
32﹣22=2×2+1②,
42﹣32=2×3+1③,
……,
(n+1)2﹣n2=2n+1,
∴将①+②+③+…,得(n+1)2﹣12=2(1+2+3+…+n)+nn2+2n=2S1+n,
∴S1=![]() .
.

 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案【题目】某班男生分成甲、乙两组进行引体向上的专项训练,已知甲组有![]() 名男生,并对两组男生训练前、后引体向上的个数进行统计分析,得到乙组男生训练前、后引体向上的平均个数分别是
名男生,并对两组男生训练前、后引体向上的个数进行统计分析,得到乙组男生训练前、后引体向上的平均个数分别是![]() 个和
个和![]() 个,及下面不完整的统计表和统计图.
个,及下面不完整的统计表和统计图.
甲组男生训练前、后引体向上个数统计表(单位:个)
甲组 | 男生 | 男生 | 男生 | 男生 | 男生 | 男生 | 平均个数 | 众数 | 中位数 |
训练前 |
|
|
|
|
|
|
|
|
|
训练后 |
|
|
|
|
|
|
|
|
|
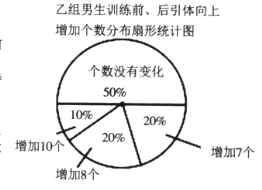
根据以上信息,解答下列问题:
(1)![]() ,
,![]() ,
,![]() ;
;
(2)甲组训练后引体向上的平均个数比训练前增长了 ![]() ;
;
(3)你认为哪组训练效果好?并提供一个支持你观点的理由;
(4)小华说他发现了一个错误:“乙组训练后引体向上个数不变的人数占该组人数的![]() ,所以乙组的平均个数不可能提高
,所以乙组的平均个数不可能提高![]() 个这么多.”你同意他的观点吗?说明理由.
个这么多.”你同意他的观点吗?说明理由.
【题目】某次数学竞赛中有5道选择题,每题1分,每道题在![]() 、
、![]() 、
、![]() 三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 | 第二题 | 第三题 | 第四题 | 第五题 | 得分 | |
甲 |
|
|
|
|
| 4 |
乙 |
|
|
|
|
| 3 |
丙 |
|
|
|
|
| 2 |
丁 |
|
|
|
|
|
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可).