题目内容
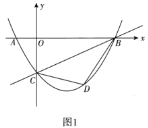
【题目】如图在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,二次函数
,二次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,动点
,动点![]() 在直线
在直线![]() 下方的二次函数图象上.
下方的二次函数图象上.
(1)求二次函数的表达式;
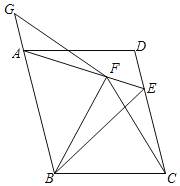
(2)如图1,连接![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
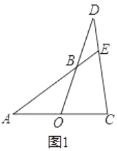
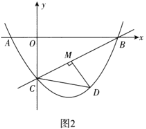
(3)如图2,过点![]() 作
作![]() 于点
于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,直接写出点
的2倍?若存在,直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】1)![]() ;(2)S最大值为4;(3)存在,点D的横坐标为2或
;(2)S最大值为4;(3)存在,点D的横坐标为2或![]()
【解析】
(1)根据题意得到B、C两点的坐标,设抛物线的解析式为![]() ,将点C的坐标代入求得m的值即可;
,将点C的坐标代入求得m的值即可;
(2)过点D作DF⊥x轴,交BC与点F,设![]() ,则
,则![]() ,然后列出S与x的关系式,最后利用配方法求得其最大值即可;
,然后列出S与x的关系式,最后利用配方法求得其最大值即可;
(3)根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点E,EA=EC=EB=![]() ,过D作Y轴的垂线,垂足为R,交AC的延线于G,设
,过D作Y轴的垂线,垂足为R,交AC的延线于G,设![]() ,则DR=x,
,则DR=x,![]() ,最后,分为∠DCM=2∠BAC和∠MDC=2∠BAC两种情况列方程求解即可.
,最后,分为∠DCM=2∠BAC和∠MDC=2∠BAC两种情况列方程求解即可.
:(1)把x=0代入![]() 得y=-2,
得y=-2,
∴C(0,-2).
把y=0代![]() 得x=4,
得x=4,
∴B(4,0),
设抛物线的解析式为![]() ,将C(0,-2)代入得:2m=-2,解得:m=-1,∴A(-1,0).
,将C(0,-2)代入得:2m=-2,解得:m=-1,∴A(-1,0).
∴抛物线的解析式![]() ,即
,即![]() ;
;
(2)如图所示:过点D作DF⊥x轴,交BC与点F.
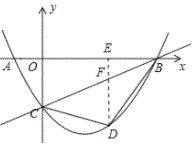
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴当x=2时,S有最大值,最大值为4.
(3)如图所示:过点D作DR⊥y垂足为R,DR交BC与点G.
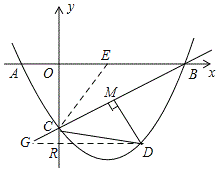
∵A(-1,0),B(4,0),C(0,-2),
∴![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴△ABC为直角三角形.
取AB的中点E,连接CE,则CE=BE,
∴∠OEC=2∠ABC.
∴![]() ,
,
当∠MCD=2∠ABC时,则tan∠CDR=tan∠ABC= ![]() ,
,
设![]() ,则DR=x,
,则DR=x,![]() ,
,
∴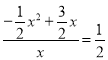 ,解得:x=0(舍去)或x=2.
,解得:x=0(舍去)或x=2.
∴点D的横坐标为2.
当∠CDM=2∠ABC时,设MD=3k,CM=4k,CD=5k.
∵tan∠MGD= ![]() ,
,
∴GM=6k,![]() ,
,
∴GC=MG-CM=2k,
∴![]() ,
,
∴![]() ,
,
∴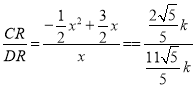 ,整理得:
,整理得:![]() ,
,
解得:x=0(舍去)或x=![]() .
.
∴点D的横坐标为![]() ,
,
综上所述,当点D的横坐标为2或![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某次数学竞赛中有5道选择题,每题1分,每道题在![]() 、
、![]() 、
、![]() 三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 | 第二题 | 第三题 | 第四题 | 第五题 | 得分 | |
甲 |
|
|
|
|
| 4 |
乙 |
|
|
|
|
| 3 |
丙 |
|
|
|
|
| 2 |
丁 |
|
|
|
|
|
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可).