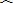题目内容
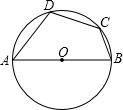
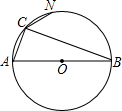
已知，如图，优弧
的度数为280°，D是由弦AB与优弧
所围成的弓形区域内的任意点，连接AD、BD．试判断∠ADB的度数范围？并说明理由．
 |
| ACB |
|
| ACB |
∠ADB的度数范围为：40°＜∠ADB＜180°，（2分）
理由为：延长AD交
于E点，连接EB，（2分）
∵
=280°，
∴∠AEB=
（360°-
）=40°，（2分）
又∵∠ADB为△BDE的外角，
∴∠ADB=∠AEB+∠EBD＞∠AEB，且∠ADB＜180°，（2分）
则40°＜∠ADB＜180°．
（说理过程中结论完整不扣分，如最后结论不全则需倒扣1分）
理由为：延长AD交
|
| ACB |
∵
|
| ACB |
∴∠AEB=
| 1 |
| 2 |
|
| ACB |
又∵∠ADB为△BDE的外角，
∴∠ADB=∠AEB+∠EBD＞∠AEB，且∠ADB＜180°，（2分）
则40°＜∠ADB＜180°．
（说理过程中结论完整不扣分，如最后结论不全则需倒扣1分）
练习册系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
