题目内容
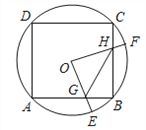
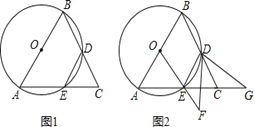
【题目】如图1,已知△ABC,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.
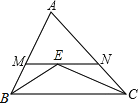
(1)求证:DE=DC.
(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系.
【答案】(1)证明见试题解析;(2)DF=DG.
【解析】
(1)利用院内接四边形的性质得到∠DEC=∠B,然后利用等角对等边得到结论.
(2)利用旋转的性质及圆内接四边形的性质证得△EDF≌△CDG后即可得到结论.
(1)∵四边形ABDE内接于⊙O,
∴∠B+∠AED=180°,
∵∠DEC+∠AED=180°,
∴∠DEC=∠B,
∵AB=AC,
∴∠C=∠B,
∴∠DEC=∠C,
∴DE=DC;
(2)∵四边形ABDE内接于⊙O,
∴∠A+∠BDE=180°,
∵∠EDC+∠BDE=180°,
∴∠A=∠EDC,
∵OA=OE,∴∠A=∠OEA,
∵∠OEA=∠CEF,∴∠A=∠CEF,∴∠EDC=∠CEF,
∵∠EDC+∠DEC+∠DCE=180°,∴∠CEF+∠DEC+∠DCE=180°,即∠DEF+∠DCE=180°,
又∵∠DCG+∠DCE=180°,∴∠DEF=∠DCG,
∵∠EDC旋转得到∠FDG,∴∠EDC=∠FDG,
∴∠EDC﹣∠FDC=∠FDG﹣∠FDC,即∠EDF=∠CDG,
∵DE=DC,∴△EDF≌△CDG(ASA),
∴DF=DG.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目