题目内容
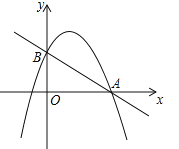
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,交AB于点F,DF=BF,EA=EF.

(1)求证:△AEF为等边三角形;
(2)若CF⊥AB,①试说明DC = CF;②求AD的长.
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)根据直径可得![]() ,再根据等腰三角形和外角定理可得
,再根据等腰三角形和外角定理可得![]() ,再根据EF=EA,即可得到结果;
,再根据EF=EA,即可得到结果;
(2)①连接OC,则OA=OC,由(1)可得![]() ,得到三角形AOC是等边三角形,再由CF⊥AB,根据三线合一的性质可得到角的关系,即可得到结果;②根据已知条件证明
,得到三角形AOC是等边三角形,再由CF⊥AB,根据三线合一的性质可得到角的关系,即可得到结果;②根据已知条件证明![]() ,可得
,可得![]() ,根据勾股定理即可得到结果.
,根据勾股定理即可得到结果.
(1)证明:由图可知。
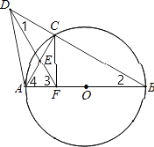
∵AB是![]() O的直径
O的直径
∴![]() ,
,
∴![]() ,
,
∵DF=BF,
∴![]() ,
,
∴![]() ,
,
∵EA=EF,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵EF=EA,
∴△AEF是等边三角形.
(2)①如图所示,
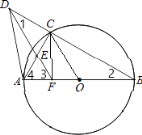
连接OC,则OA=OC,由(1)可得![]() ,
,
∴三角形AOC是等边三角形,
又∵CF⊥AB,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴CD=CF.
②由题可得圆的半径为1,
由①可得:![]() ,
,![]() ,
,
∴![]() ,
,
∴AC=OC=CA=1,
∴![]() ,
,
∴![]() ,
,
∴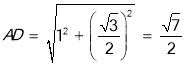 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校鼓励师生利用课余时间广泛阅读,为了解学生课外阅读情况,抽样调查了部分学生每周用于课外阅读的时间,过程如下:
数据收集:从全校随机抽取20名学生,进行了每周用于课外阅读时间的调查,数据如下单位:min)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
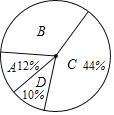
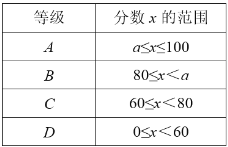
分段整理样本数据:
课外阅读时间 |
|
|
|
|
等级 | D | C | B | A |
人数 | 3 | ① | 8 | ② |
统计量:
平均数 | 中位数 | 众数 |
80 | ③ | ④ |
得出结论:
(1)填写表格中的数据:
(2)如果该校现有学生400人,估计等级为“B”的学生有多少名?
(3)假设平均阅读一本课外书的时间为160分钟,请你选择样本中的一种统计量估计该校学生每人一年(按52周计算)平均阅读多少本课外书?