��Ŀ����
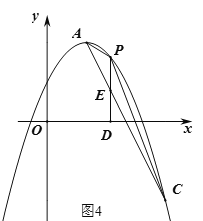
����Ŀ�����壺������������������߶ν������ߵ��ң���������֮���������ϵ�����һ��P������㹹�ɵ������γ��������ߵ������ǣ���P�����������P�ĺ�����Ϊx��
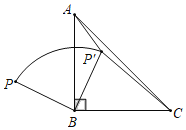
��֪�����߾���A��1��2����B��m��n����C��3����2�����㣬P����������AC֮���һ�㣬��ACΪ�ҵ�������Ϊ��PAC.
��1��ͼһ����m��2��n��1ʱ����������ߵĽ���ʽ����x��k1ʱ��PAC����������k1��ֵ��
��2��ͼ������m��2��n��1ʱ����n��ʾ�������ߵĽ���ʽ����x��k2ʱ��PAC����������k2��ֵ��k1��k2�к�������ϵ��
��3��ͼ������m��2��n��1ʱ����m��n��ʾ�������ߵĽ���ʽ����x��k3ʱ��PAC����������k3��ֵ���۲�ͼ1��2��3��������A��C������B�ڸ��ֲ�ͬλ�����ü��������㷢��ͨ�����������������ϵ�У��Դ�����Ϊ�ҵ������ǵ����ȡ�����ֵʱ�����ĺ������кι��ɣ�
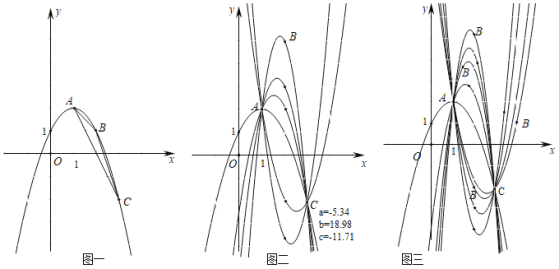
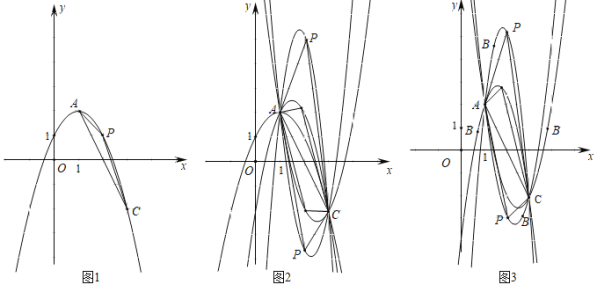
���𰸡���1��y����x2+2x+1��k1��2����2��y����nx2+��4n��2��x+��4��3n����k2��2��k1��k2����3��![]() ��k3��2�����ĺ��������ȣ�
��k3��2�����ĺ��������ȣ�
��������
��1�����ݴ���ϵ������⼴�ɣ�����P��PD��x���ڵ�D����ֱ��AC�ڵ�E����ͼ4�������ֱ��AC�Ľ���ʽ�����ڵ�P�ĺ�����Ϊk1������������͵�E��������ɵã�����PE�ij�����k1�Ĵ���ʽ��ʾ��Ȼ������![]() �ɵá�PAC���������k1�ĺ�����ϵʽ�������ö��κ�����������⼴�ɣ�
�ɵá�PAC���������k1�ĺ�����ϵʽ�������ö��κ�����������⼴�ɣ�
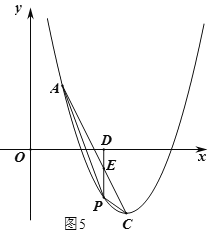
��2���ȸ��ݴ���ϵ������������ߵĽ���ʽ�����ݵ�B��λ�����������ۣ�����n>0����ͼ4���£�1�����˼·��k2�Ĵ���ʽ��ʾ��PE�ij���Ȼ������![]() �ɵ���PAC���������k2�ĺ�����ϵʽ�������ö��κ�����������⼴�ɣ�����n<0����ͼ5��������˼·�ɵ�
�ɵ���PAC���������k2�ĺ�����ϵʽ�������ö��κ�����������⼴�ɣ�����n<0����ͼ5��������˼·�ɵ�![]() ����������k2�Ĵ���ʽ��ʾ����PAC������������ö��κ�����������⼴�ɣ���һ�����ɱȽ�k1��k2��������ϵ��
����������k2�Ĵ���ʽ��ʾ����PAC������������ö��κ�����������⼴�ɣ���һ�����ɱȽ�k1��k2��������ϵ��
��3���ȸ��ݴ���ϵ������������ߵĽ���ʽ��Ȼ��£�2�����˼·����������ɵá�PAC���������k3�ĺ�����ϵʽ�������ö��κ�����������⼴�ɣ�Ȼ�����ǰ��3��С��Ľ�����ɵó����ĺ�����Ĺ��ɣ�
�⣺�������ߵĽ���ʽΪy��ax2+bx+c��
��1����m��2��n��1ʱ����A��1��2����B��2��1����C��3����2�����룬��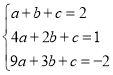 ����ã�
����ã�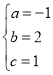 ��
��
�������ߵĽ���ʽΪ��y����x2+2x+1��
��A��1��2����C��3����2������ֱ��AC�Ľ���ʽΪy����2x+4��
��P��k1����k12+2k1+1��������P��PD��x���ڵ�D����ֱ��AC�ڵ�E����ͼ4�����E��k1����2k1+4����
��![]() ��
��
��![]() ��
��
�൱k1��2ʱ����PAC��������
��2����m��2��n��1ʱ����A��1��2����B��2��n����C��3����2�����룬�ã�
 ����ã�
����ã� ��
��
�������ߵĽ���ʽΪ��y����nx2+��4n��2��x+��4��3n����
����n>0����P��k2����nk22+��4n��2��k2+(4��3n)��������P��PD��x���ڵ�D����ֱ��AC�ڵ�E����ͼ4�����E��k2����2k2+4����
��![]() =��nk22+��4n��2��k2+(4��3n)+2k2��4=��nk22+4nk2��3n��
=��nk22+��4n��2��k2+(4��3n)+2k2��4=��nk22+4nk2��3n��
��![]() ��
��
�൱k2��2ʱ����PAC��������
����n<0����ͼ5����![]() =��2k2+4+nk22����4n��2��k2��(4��3n)=nk22��4nk2+3n��
=��2k2+4+nk22����4n��2��k2��(4��3n)=nk22��4nk2+3n��
��![]() ��
��
�൱k2��2ʱ����PAC��������
���ϣ���k2��2ʱ����PAC��������
��k1��k2��
��3����m��2��n��1ʱ����A��1��2����B��m��n����C��3����2�����룬�ã�
 ����ã�
����ã�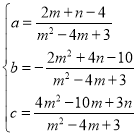 ��
��
�������ߵĽ���ʽΪ��![]() ��
��
��P��k3��![]() ����
����
����![]() ������P��PD��x���ڵ�D����ֱ��AC�ڵ�E����ͼ4�����E��k3����2k3+4����
������P��PD��x���ڵ�D����ֱ��AC�ڵ�E����ͼ4�����E��k3����2k3+4����
��![]() =
=![]() =
=![]() ��
��
��![]() ��
��
�൱k3��2ʱ����PAC��������
����![]() ����ͼ5����
����ͼ5����![]() =
=![]()
![]() ��
��
��![]() ��
��
�൱k3��2ʱ����PAC��������
���ϣ���k3��2ʱ����PAC��������
����������������A��C������B�ڸ��ֲ�ͬλ�����ü����������Է���ͨ�����������������ϵ�У��Դ�����Ϊ�ҵ������ǵ����ȡ�����ֵʱ�����ĺ��������ȣ�

 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д� Ӧ������ҵ��ϵ�д�
Ӧ������ҵ��ϵ�д�