题目内容
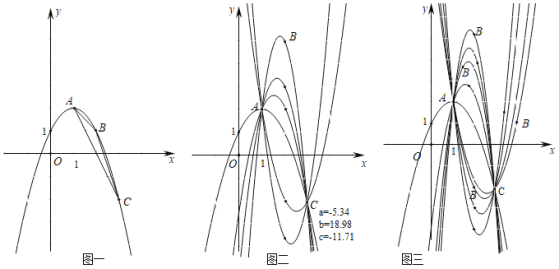
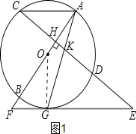
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F.切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
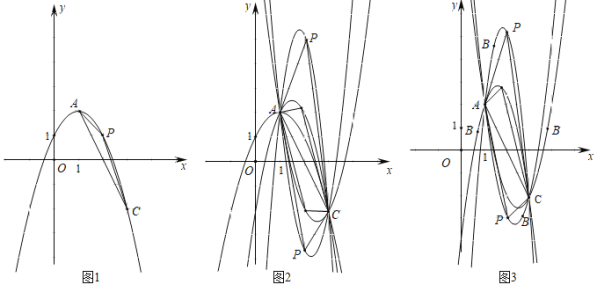
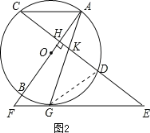
(2)如图2,若AC∥EF,试判断线段KG、KD、GE间的数量关系,并说明理由;
(3)在(2)的条件下,若sinE=![]() ,AK=2
,AK=2![]() ,求⊙O的半径.
,求⊙O的半径.

【答案】(1)见解析;(2)KG2=KDGE,见解析;(3)![]()
【解析】
(1)如图1,连接OG.根据切线性质及CD⊥AB,可以推出∠KGE=∠AKH=∠GKE,根据等角对等边得到KE=GE;
(2)如图2,根据平行得角相等,证明△GKD∽△EFG,列比例式可得结论;
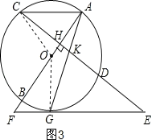
(3)如图3所示,连接OG,OC,由(1)得KE=GE,根据sinE![]() ,设AH=3t,则AC=5t,CH=4t,列式先求t的值,再求出圆的半径.
,设AH=3t,则AC=5t,CH=4t,列式先求t的值,再求出圆的半径.
(1)如图1,连接OG.
∵EG为切线,
∴∠KGE+∠OGA=90°.
∵CD⊥AB,
∴∠AKH+∠OAG=90°.
又∵OA=OG,
∴∠OGA=∠OAG,
∴∠KGE=∠AKH=∠GKE,
∴KE=GE.
(2)KG2=KDGE.理由如下:
连接GD,如图2.
∵AC∥EF,
∴∠C=∠E.
∵∠C=∠AGD,
∴∠E=∠AGD.
∵∠GKD=∠GKD,
∴△GKD∽△EKG,
∴![]() ,
,
∴KG2=KDEK,
由(1)得:EK=GE,
∴KG2=KDGE;
(3)连接OG,OC,如图3所示,
由(1)得:KE=GE.
∵AC∥EF,
∴∠E=∠ACH.
∵sinE=sin∠ACH![]() ,
,
设AH=3t,则AC=5t,CH=4t.
∵KE=GE,AC∥EF,
∴CK=AC=5t,
∴HK=CK﹣CH=t.
在Rt△AHK中,根据勾股定理得AH2+HK2=AK2,
即(3t)2+t2![]() ,解得:t
,解得:t![]() .
.
设⊙O半径为r.在Rt△OCH中,OC=r,OH=r﹣3t,CH=4t,
由勾股定理得:OH2+CH2=OC2,
即(r﹣3t)2+(4t)2=r2,解得:r![]() t
t![]() ,
,
答:⊙O的半径为![]() .
.

【题目】我市某公司用800万元购得某种产品的生产技术后,进一步投入资金1550万元购买生产设备,进行该产品的生产加工,已知生产这种产品每件还需成本费40元.经过市场调研发现:该产品的销售单价需要定在200元到300元之间较为合理.销售单价![]() (元)与年销售量
(元)与年销售量![]() (万件)之间的变化可近似的看作是如下表所反应的一次函数:
(万件)之间的变化可近似的看作是如下表所反应的一次函数:
销售单价 | 200 | 230 | 250 |
年销售量 | 14 | 11 | 9 |
(1)请求出![]() 与
与![]() 之间的函数关系式,并直接写出自变量
之间的函数关系式,并直接写出自变量![]() 的取值范围;
的取值范围;
(2)请说明投资的第一年,该公司是盈利还是亏损?若盈利,最大利润是多少?若亏损,最少亏损是多少?