Question

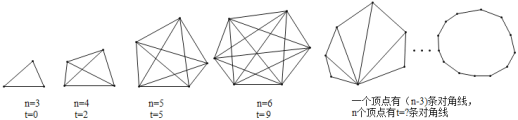
【题目】如图，先研究下面三角形、四边形、五边形、六边形…多边形的边数n及其对角线条数t的关系，再完成下面问题：

（1）若一个多边形是七边形，它的对角线条数为　 　，n边形的对角线条数为t＝　 　（用n表示）．

（2）求正好65条对角线的多边形是几边形．

Answer 1

【答案】（1）14，；（2）13．

【解析】

（1）根据从一个顶点出发的对角线条数乘以多边形的边数再除以2解答即可；

（2）设正好65条对角线的多边形是x边形，根据（1）题的公式可得关于x的方程，解方程即可求出结果．

解：（1）若一个多边形是七边形，它的对角线条数为，n边形的对角线条数为．

故答案为：14，；

（2）设正好65条对角线的多边形是x边形，依题意有：，解得x1＝13，x2＝﹣10（舍去）．

故正好65条对角线的多边形是13边形．