Question

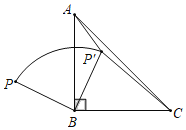
【题目】如图，P是等腰直角△ABC外一点，把BP绕点B顺时针旋转90°到BP′，使点P′在△ABC内，已知∠AP′B＝135°，若连接P′C，P′A：P′C＝1：4，则P′A：P′B＝（　　）

A.1：4B.1：5C.2：D.1：

Answer 1

【答案】C

【解析】

连接AP，根据同角的余角相等可得∠ABP＝∠CBP′，然后利用“边角边”证明△ABP和△CBP′全等，根据全等三角形对应边相等可得AP＝CP′，连接PP′，根据旋转的性质可得△PBP′是等腰直角三角形，然后求出∠AP′P是直角，再利用勾股定理用AP′表示出PP′，又等腰直角三角形的斜边等于直角边的倍，代入整理即可得解．

解：如图，连接AP，

∵BP绕点B顺时针旋转90°到BP′，

∴BP＝BP′，∠ABP+∠ABP′＝90°，

又∵△ABC是等腰直角三角形，

∴AB＝BC，∠CBP′+∠ABP′＝90°，

∴∠ABP＝∠CBP′，

在△ABP和△CBP′中，

∵，

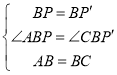∴△ABP≌△CBP′（SAS），

∴AP＝P′C，

∵P′A：P′C＝1：4，

∴AP＝4P′A，

连接PP′，则△PBP′是等腰直角三角形，

∴∠BP′P＝45°，PP′＝PB，

∵∠AP′B＝135°，

∴∠AP′P＝135°﹣45°＝90°，

∴△APP′是直角三角形，

设P′A＝x，则AP＝4x，

∴PP'＝，

∴P'B＝PB＝，

∴P′A：P′B＝2：，

故选：C．