题目内容
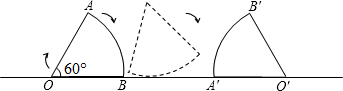
如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①∠EAF=45°；②△ADE≌△AFE；③EF=ED；④BE2+DC2=DE2．其中正确的个数是（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
∵△ADC绕点A顺时针90°旋转后，得到△AFB，
∴∠FAD=90°，DC=BF，∠FBE=90°，AD=AF，
∵∠DAE=45°，
∴∠EAF=90°-45°=45°，
∴△DAE≌△FAE，
∴EF=ED，
在Rt△BEF中，BE2+BF2=EF2，
∴BE2+DC2=DE2．
∴①②③④正确．
故选D．
∴∠FAD=90°，DC=BF，∠FBE=90°，AD=AF，
∵∠DAE=45°，
∴∠EAF=90°-45°=45°，
∴△DAE≌△FAE，
∴EF=ED，
在Rt△BEF中，BE2+BF2=EF2，
∴BE2+DC2=DE2．
∴①②③④正确．
故选D．
练习册系列答案
相关题目
0°得到线段OP′
