题目内容
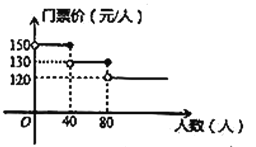
【题目】我市某风景区门票价格如图所示,有甲、乙两个旅行团队,计划在端午节期间到该景点游玩,两团队游客人数之和为100人,乙团队人数不超过40人.设甲团队人数为![]() 人,如果甲、乙两团队分别购买门票,两团队门票款之和为
人,如果甲、乙两团队分别购买门票,两团队门票款之和为![]() 元.
元.
(1)直接写出![]() 关于
关于![]() 的函数关系式,并写出自变
的函数关系式,并写出自变![]() 的取值范围;
的取值范围;
(2)若甲团队人数不超过80人,计算甲、乙两团队联合购票比分别购票最多可节约多少钱?
(3)端午节之后,该风景区对门票价格作了如下调整:人数不超过40人时,门票价格不变,人数超过40人但不超过80人时,每张门票降价![]() 元;人数超过80人时,每张门票降价
元;人数超过80人时,每张门票降价![]() 元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求
元.在(2)的条件下,若甲、乙两个旅行团端午节之后去游玩联合购票比分别购票最多可节约3900元,求![]() 的值.
的值.
【答案】(1)当![]() 时,
时, ![]() ;当
;当![]() 时,
时,![]() ;(2)甲、乙两团队联合购票比分别购票最多可节约1800元;(3)
;(2)甲、乙两团队联合购票比分别购票最多可节约1800元;(3)![]() 的值为15.
的值为15.
【解析】
(1)由乙团队人数不超过40人,讨论x的取值范围,得到分段函数;
(2)由(1)在甲团队人数不超过80人时,讨论的最大值与联合购票费用相减即可;
(3)在(2)的基础上在购票单价减去a元,经过讨论,得到含有a的购票最大费用,两个团队联合购票费用为100(120-2a),根据题意构造方程.
解:(1)由题意乙团队人数为![]() 人,
人,
则![]() ,
,
![]() ,
,
当![]() 时,
时,
![]()
当![]() 时,
时,
![]()
(2)由(1)
甲团队人数不超过80人
∵![]() ,
,
∴![]() 随
随![]() 增大而减小,
增大而减小,
∴当![]() 时,
时,![]() ,
,
当两团队联合购票时购票费用为
![]()
甲、乙两团队联合购票比分别购票最多可节约![]() 元.
元.
(3)在(2)的条件下
当![]() 时,
时,
![]()
∵![]() ,
,
∴![]() 随
随![]() 增大而减小,
增大而减小,
∴当![]() 时,
时,![]() ,
,
由价格方案,联合购票费用为![]() ,
,
∴![]() ,
,
解得![]() ,
,
答:![]() 的值为15.
的值为15.

练习册系列答案
相关题目