题目内容
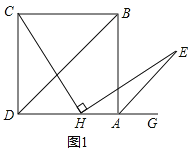
【题目】如图,在矩形ABCD中AD=12,AB=9,E为AD的中点,G是DC上一点,连接BE,BG,GE,并延长GE交BA的延长线于点F,GC=5
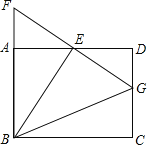
(1)求BG的长度;
(2)求证:![]() 是直角三角形
是直角三角形
(3)求证:![]()
【答案】(1)13(2)见解析(3)见解析
【解析】
(1)在Rt△BCG中利用勾股定理即可求解;
(2)利用勾股定理依次求出BE,EG,再利用勾股定理逆定理即可证明;
(3)由E点为AD中点得到E为FG中点,再根据BE⊥FG得到△BFG为等腰三角形,得到∠F=∠BGF,再根据平行线的性质即可证明.
(1)∵四边形ABCD为矩形,∴BC=AD=12,∠C=90°,
∴BG=![]()
(2)∵E为AD中点,∴AE=DE=6,
∴BE=![]()
∵DG=CD-GC=4,
∴EG=![]()
∴BG2=DG2+EG2,
∴![]() 是直角三角形
是直角三角形
(3)∵AE=DE,∠FAE=∠D=90°,又∠AEF=∠DEG,
∴△AEF≌△DEG,
∴E为EG中点,又BE⊥FG,
∴△BFG为等腰三角形,
∴∠F=∠BGF,
又BF∥CD,
∴∠F=![]()
∴![]()

【题目】“水是生命之源”,某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
用水量/月 | 单价(元/m3) |
不超过20m3 | 2.8 |
超过20m3的部分 | 3.8 |
另:每立方米用水加收0.2元的城市污水处理费 | |
(1)根据上表,用水量每月不超过20m3,实际每立方米收水费_____元;如果1月份某用户用水量为19m3,那么该用户1月份应该缴纳水费____元;
(2)某用户2月份共缴纳水费80元,那么该用户2月份用水多少m3?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,问该用户3月份实际应该缴纳水费多少元?
【题目】如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标、点B的横坐标如图所示.
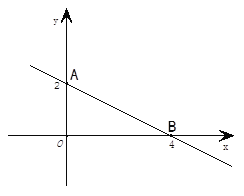
(1)求直线AB的解析式;
(2)点P在直线AB上,是否存在点P使得△AOP的面积为1,如果有请直接写出所有满足条件的点P的坐标