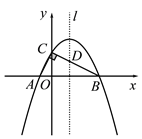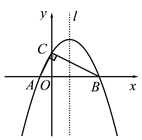题目内容
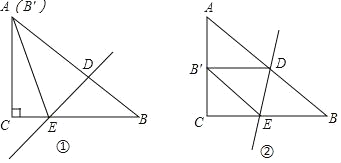
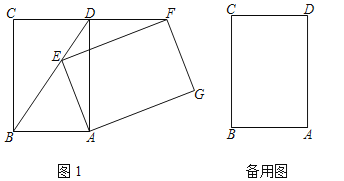
【题目】(1)探索发现:如图1,已知Rt△ABC中,∠ACB=90°,AC=BC,直线l过点C,过点A作AD⊥l,过点B作BE⊥l,垂足分别为D、E.求证:AD=CE,CD=BE.
(2)迁移应用:如图2,将一块等腰直角的三角板MON放在平面直角坐标系内,三角板的一个锐角的顶点与坐标原点O重合,另两个顶点均落在第一象限内,已知点M的坐标为(1,3),求点N的坐标.
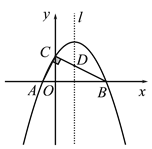
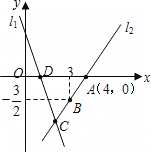
(3)拓展应用:如图3,在平面直角坐标系内,已知直线y=﹣3x+3与y轴交于点P,与x轴交于点Q,将直线PQ绕P点沿逆时针方向旋转45°后,所得的直线交x轴于点R.求点R的坐标.

【答案】(1)见解析(2)(4,2)(3)(6,0)
【解析】
(1)先判断出∠ACB=∠ADC,再判断出∠CAD=∠BCE,进而判断出△ACD≌△CBE,即可得出结论;
(2)先判断出MF=NG,OF=MG,进而得出MF=1,OF=3,即可求出FG=MF+MG=1+3=4,即可得出结论;
(3)先求出OP=3,由y=0得x=1,进而得出Q(1,0),OQ=1,再判断出PQ=SQ,即可判断出OH=4,SH=0Q=1,进而求出直线PR的解析式,即可得出结论.
证明:∵∠ACB=90°,AD⊥l
∴∠ACB=∠ADC
∵∠ACE=∠ADC+∠CAD,∠ACE=∠ACB+∠BCE
∴∠CAD=∠BCE,
∵∠ADC=∠CEB=90°,AC=BC
∴△ACD≌△CBE,
∴AD=CE,CD=BE,

(2)解:如图2,过点M作MF⊥y轴,垂足为F,过点N作NG⊥MF,交FM的延长线于G,
由已知得OM=ON,且∠OMN=90°
∴由(1)得MF=NG,OF=MG,
∵M(1,3)
∴MF=1,OF=3
∴MG=3,NG=1
∴FG=MF+MG=1+3=4,
∴OF﹣NG=3﹣1=2,
∴点N的坐标为(4,2),

(3)如图3,过点Q作QS⊥PQ,交PR于S,过点S作SH⊥x轴于H,
对于直线y=﹣3x+3,由x=0得y=3
∴P(0,3),
∴OP=3
由y=0得x=1,
∴Q(1,0),OQ=1,
∵∠QPR=45°
∴∠PSQ=45°=∠QPS
∴PQ=SQ
∴由(1)得SH=OQ,QH=OP
∴OH=OQ+QH=OQ+OP=3+1=4,SH=OQ=1
∴S(4,1),
设直线PR为y=kx+b,则![]() ,解得
,解得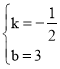
∴直线PR为y=﹣![]() x+3
x+3
由y=0得,x=6
∴R(6,0).

 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案