题目内容
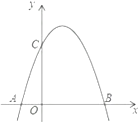
【题目】如图,是将抛物线y=-x2 平移后得到的抛物线,其对称轴为x=1,与x轴的一个交点为A(-1,0) ,另一交点为B,与y轴交点为C.
(1)求抛物线的函数表达式;
(2)若点N 为抛物线上一点,且BC⊥NC,求点N的坐标;
(3)点P是抛物线上一点,点Q是一次函数y=![]() x+
x+![]() 的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
的图象上一点,若四边形OAPQ为平行四边形,这样的点P、Q是否存在?若存在,分别求出点P、Q的坐标,若不存在,说明理由.
【答案】(1)y=-x2+2x+3;(2)(1,4); (3)P、Q的坐标是(0,3)(1,3) 或![]() ,
,![]() .
.
【解析】试题分析:
(1)由题意可设该抛物线的解析式为![]() ,代入点(-1,0)求出k的值即可得到所求解析式;
,代入点(-1,0)求出k的值即可得到所求解析式;
(2)由(1)中所得抛物线的解析式可求得点B、C的坐标,从而可求出直线BC的解析式,由直线NC⊥BC且过点C可求得NC的解析式,把NC的解析式和抛物线的解析式联立得到方程组,解方程组即可求得点N的坐标;
(3)如下图,由题意易得PQ=OA=1,且PQ∥OA,设点P的横坐标为t,则可用含“t”的式子表达出Q的坐标,再把Q的坐标代入函数y=![]() x+
x+![]() 中,即可解得“t”的值,从而可求得P、Q的坐标.
中,即可解得“t”的值,从而可求得P、Q的坐标.
试题解析:
(1)设抛物线的解析式是y=-(x-1)2+4.把 (-1,0)代入得 0=-(1-1)2+k,
解得,k=4
则抛物线的解析式是 y=-(x-1)2+4,
即y=-x2+2x+3;
(2)设直线BC的解析式为y=kx+b(k≠0),代入点B、C的坐标得:
![]() 解得:
解得: ![]() ,
,
∴直线BC的解析式为:y=-x+3,
∵BC⊥NC,
∴可设直线CN的解析式为y=x+m.
∵C(0,3)在直线CN上,
∴0+m=3,解得:m=3,即直线CN的解析式为 y=x+3,
由: ![]() ,即 x+3=-x2+2x+3=-x2+2x+3,解得:x1=0,x2=1,
,即 x+3=-x2+2x+3=-x2+2x+3,解得:x1=0,x2=1,
∴N的坐标是(1,4),

(3)∵四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,
设P(t,-t2+2t+3),则Q(t+1, -t2+2t+3) ,将P、Q的坐标代入![]() ,
,
得-t2+2t+3=![]() ,
,
整理,得2t2-t=0, ,
解得t=0 或![]() .
.
∴-t2+2t+3 的值为3或![]() .
.
∴P、Q的坐标是(0,3)(1,3) 或![]() ,
,![]() .
.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】为了让更多的失学儿童重返校园,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
组别 | 捐款额(x)元 | 户数 |
A | 1≤x<50 | a |
B | 50≤x<100 | 10 |
C | 100≤x<150 | |
D | 150≤x<200 | |
E | x≥200 |
请结合以上信息解答下列问题.

(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区有1500户住户,请根据以上信息估计,全社区捐款不少于150元的户数是多少?
【题目】为了解某校学生的身高情况,王老师随机抽取该校男生、女生进行抽样调查,已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计图表:
组别 | 身高 |
|
|
|
|
|
|
|
|
|
|
身高情况分组表
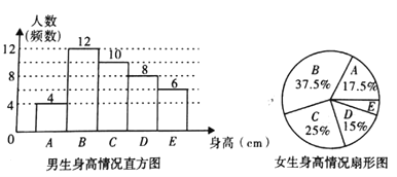
根据图表提供的信息,回答下列问题:
(1)样本中,女生身高在![]() 组的人数有_________人;
组的人数有_________人;
(2)在上面的扇形统计图中,表示![]() 组的扇形的圆心角是_________°;
组的扇形的圆心角是_________°;
(3)已知该校共有男生800人,女生760人,请估计该校身高在![]() 之间的学生约有多少人?
之间的学生约有多少人?