题目内容
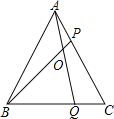
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的中点,点
边上的中点,点![]() 是
是![]() 边上的一个动点,延长
边上的一个动点,延长![]() 到
到![]() ,使
,使![]() ,作
,作![]() ,其中
,其中![]() 点在
点在![]() 上.
上.
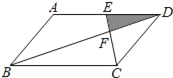
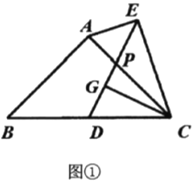
(1)如图①,若![]() ,则
,则![]() _______.
_______.
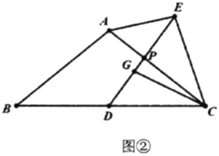
(2)如图②,若![]() ,求
,求![]() 的值;
的值;
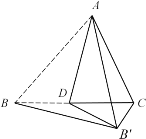
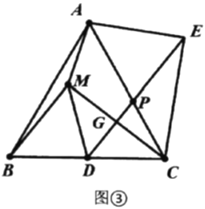
(3)如图③,若![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() ,在点
,在点![]() 运动的过程中,探究:当
运动的过程中,探究:当![]() 的值为多少时,线段
的值为多少时,线段![]() 与
与![]() 的长度和取得最小值?
的长度和取得最小值?
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3)![]()
【解析】
(1)连接AD,首先证明AC=![]() CD,再证明△DCG∽△ACE,可得
CD,再证明△DCG∽△ACE,可得![]() ;
;
(2)连接AD.证明△DCG∽△ACE,可得![]() ,设AB=AC=5k,BD=CD=4k,则AD=
,设AB=AC=5k,BD=CD=4k,则AD=![]() ,由此即可解决问题;
,由此即可解决问题;
(3)由题意,当A,M,D共线时,AM+DM的值最小.想办法证明∠GDM=∠GDC=45°,设CH=![]() ,则PC=2
,则PC=2![]() ,PH=DH=
,PH=DH=![]() ,推出AC=2CD=2(
,推出AC=2CD=2(![]() ),由此即可解决问题.
),由此即可解决问题.
(1)如图,连接AD,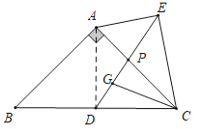
∵AB=AC,∠B=45°,
∴△ABC是等腰直角三角形,
∵BD=CD,
∴AD⊥BC,
∴AD=BD=DC,
∴AC=![]() CD,
CD,
∵∠CDE=∠CAE,∠DCG=∠ACE,
∴△DCG∽△ACE,
∴![]() ;
;
(2)如图,连接AD,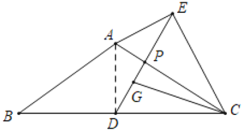
∵∠CDE=∠CAE,∠DCG=∠ACE,
∴△DCG∽△ACE,
∴![]() ,
,
∵AB=AC,BD=CD,
∴AD⊥BC,
设AB=AC=5k,BD=CD=4k,
则AD=![]() ,
,
∴![]() ;
;
(3)如图,由题意知,当A、M、D三点共线时,AM+DM的值最小.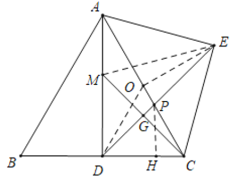
连EM,取AC的中点O,连接OE,OD,作PH⊥CD于H.
∵AB=AC,∠B=60°,
∴△ABC是等边三角形,
∴BC=AC,∠ACB=60°,
∵BD=CD,
∴AD⊥BC,
∴∠CDA=90°,
∴AC=2CD,
∵∠CDE=∠CAE,∠DCG=∠ACE,
∴△DCG∽△ACE,
∴![]() ,
,
∴EC=2CG,
∵CM=2CG,
∴CM=CE,∠DCG=∠ACE,
∵∠ACD=∠DCG+∠GCP=∠ACE+∠GCP=∠ECM=60°,
∴△ECM是等边三角形,
∵CD=CO,∠DCM=∠OCE,CM=CE,
∴△DCM≌△OCE(SAS),
∴OE=DM,
∵∠CDE=∠CAE,
∴A,D,C,E四点共圆,
∴∠ADC+∠AEC=180°,
∴∠AEC=90°,
∵OA=OC,
∴OE=OC=CD=DM,
∵CG=GM,
∴∠GDM=∠GDC=45°,
设CH=![]() ,则PC=
,则PC=![]() ,PH=DH=
,PH=DH=![]() ,
,
∴AC=2CD=2(![]() ),
),
∴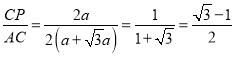 .
.