题目内容
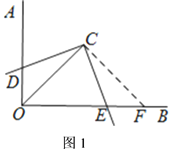
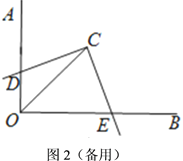
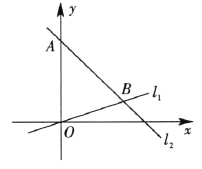
【题目】如图，在平面直角坐标系内，点
的坐标为(0，24)，经过原点的直线
与经过点的直线
相交于点
，点的坐标为(18，6).
（1）求直线，对应的函数表达式；
（2）点
为线段
上一动点（点不与点
重合），作
轴交直线于点
，设点的纵坐标为
，求点的坐标（用含的代数式表示）
【答案】（1）直线l1对应的函数表达式为y＝
x，直线l2对应的函数表达式为y＝－x＋24；（2）(3a，－3a＋24)
【解析】
（1）根据待定系数法即可求解；
（2）因为点C在直线l1上，且点C的纵坐标为a，所以a＝x，得到C点坐标，再根据CD∥y轴，得到点D的横坐标为3a，进而得到D点坐标.
解：(1)设直线l1对应的函数表达式为y＝k1x，由它过点(18，6)得18k1＝6，
解得k1＝，
所以直线l1对应的函数表达式为y＝x；
设直线l2对应的函数表达式为y＝k2x＋b，
由它过点A(0，24)，B(18，6)得b＝24，18k2＋b＝6，解得k2＝－1，
所以直线l2对应的函数表达式为y＝－x＋24
(2)因为点C在直线l1上，且点C的纵坐标为a，所以a＝x.
所以x＝3a，故点C的坐标为(3a，a)．
因为CD∥y轴， 所以点D的横坐标为3a.
因为点D在直线l2上，所以点D的纵坐标为－3a＋24.
所以点D的坐标为(3a，－3a＋24)．
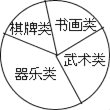
【题目】某校学生会准备调查六年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数．
（1）确定调查方式时，甲同学说：“我到六年级（1）班去调查全体同学”；乙同学说：“放学时我到校门口随机调查部分同学”；丙同学说：“我到六年级每个班随机调查一定数量的同学”．请指出哪位同学的调查方式最合理．
类别 | 频数（人数） | 频率 |
武术类 | 0.25 | |
书画类 | 20 | 0.20 |
棋牌类 | 15 | b |
器乐类 | ||
合计 | a | 1.00 |
（2）他们采用了最为合理的调查方法收集数据，并绘制了如图所示的统计表和扇形统计图．
请你根据以上图表提供的信息解答下列问题：
①a=_____，b=_____；
②在扇形统计图中，器乐类所对应扇形的圆心角的度数是_____；
③若该校六年级有学生560人，请你估计大约有多少学生参加武术类校本课程．
