Question

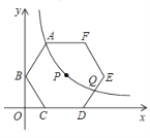
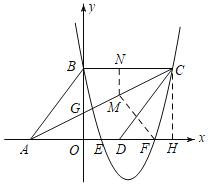
【题目】如图，在平面直角坐标系中，菱形ABCD的三个顶点A，B，D在坐标轴上，且已知点A（，），点B（，），现有抛物线m经过点B，C和OD的中点．

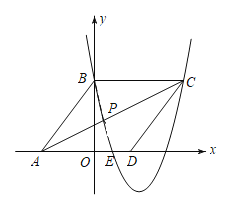
（1）求抛物线m的解析式；

（2）在抛物线上是否存在点P，使得？若存在，求出点P的坐标，若不存在，请说明理由；

（3）抛物线m与x轴的另一交点为F，M是线段AC上一动点，求的最小值．

Answer 1

【答案】（1）；（2）存在满足条件的点，使得，理由见解析；（3）

【解析】

（1）先求出点C和点D的坐标，再求出点E的坐标，设出函数m的解析式，把B、E、C三点坐标代入解析式进行求解即可；

（2）点是抛物线和直线的交点，求出AC的解析式，联立方程组，解出方程组进行取舍即可得点P坐标；

（3）过作轴于，过作于，证明△AOG∽△CNM，可得，从而可得结论.

（1）∵，

∴，

∴，即菱形的长为5，

∴，

∴，

∴OD的中点坐标为：

设抛物线的解析式为：，则

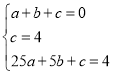，解得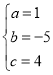

∴抛物线的解析式为．

（2）存在满足条件的点，使得．理由如下：

①当点P在BC下方时，∵，，

∴点在菱形的对角线上，

∴点是抛物线和直线的交点，

设直线的解析式为，

∵，，，，

∴，解得，

∴直线的解析式为，

由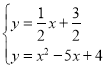解得或（舍去），

∴，．

（3）过作轴于，过作于，

∵轴，∴，

又∵，

∴△AOG∽△CNM，

∴，

∴，

∵点到最小距离为，

∴的最小值为的长度4，

∴的最小值为．