Question

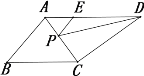
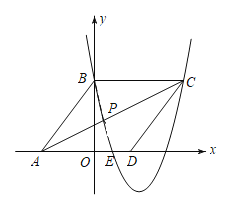
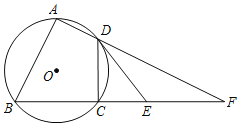
【题目】如图，四边形ABCD内接于⊙O，AB＝AC，∠BAD＝90°，延长AD，BC交于点F．过点D作⊙O的切线，交BF于点E．

（1）求证：DE＝EF；

（2）若，求的长．

Answer 1

【答案】（1）见解析；（2）

【解析】

(1)连接BD，由AB＝AC知∠ABC＝∠ADB，证∠ABC＝∠CDF得∠CDF＝∠ADB．由∠BAD＝90°知BD为⊙O的直径，据此得∠F+∠CDF＝90°，结合DE为⊙O的切线得∠ADB+∠EDF＝90°，根据∠CDF＝∠ADB得∠F＝∠EDF，从而得证；

(2)由可设EC＝3，则EF＝5，CF＝8，证△EDC～△EBD得，据此知，，BC＝，连接OB，OC，AC，AO并延长AO交BC于点H，由AB＝AC，OB＝OC知AO垂直平分BC，从而得，再由AH⊥BC，DC⊥BC知DC∥AH，得．

解：(1)连接BD，

∵AB＝AC，

∴∠ABC＝∠ADB，

∵∠ABC+∠ADC＝180°，∠CDF+∠ADC＝180°，

∴∠ABC＝∠CDF，

∴∠CDF＝∠ADB．

∵∠BAD＝90°，

∴BD为⊙O的直径，

∴∠DCB＝90°，

∴∠DCF＝90°，

∴∠F+∠CDF＝90°，

∵DE为⊙O的切线，

∴∠ODE＝90°，

∴∠ADB+∠EDF＝90°，

∵∠CDF＝∠ADB，

∴∠F＝∠EDF，

∴DE＝EF；

(2)∵，

设EC＝3，则EF＝5，CF＝3+5＝8，

∵∠BDE＝∠DCE＝90°，∠DEC＝∠DEB，

∴△EDC～△EBD，

∴，

∴，，，

∴，

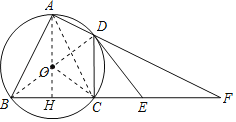
连接OB，OC，AC，AO并延长AO交BC于点H，

又∵OB＝OC，AB＝AC，

∴AO垂直平分BC，

∴，

∵AH⊥BC，DC⊥BC，

∴DC∥AH，

∴．