题目内容
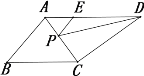
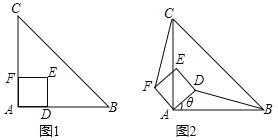
【题目】(1)问题发现:如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,点D、F分别在边AB、AC上,请直接写出线段BD、CF的数量和位置关系;
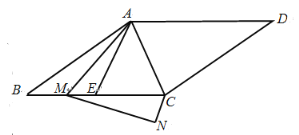
(2)拓展探究:如图2,当正方形ADEF绕点A逆时针旋转锐角θ时,上述结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)BD=CF,BD⊥CF,理由见解析;(2)成立,理由见解析.
【解析】
(1)根据等腰直角三角形的性质和正方形的性质解答即可;
(2)△ABC是等腰直角三角形,四边形ADEF是正方形,易证得△BAD≌△CAF,根据全等三角形的对边相等,即可证得BD=CF,进而证明BD⊥CF
(1)BD=CF,BD⊥CF,理由如下:
∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∴BD=CF,BD⊥CF;
(2)成立,理由如下:
∵△ABC是等腰直角三角形,四边形ADEF是正方形,
∴AB=AC,AD=AF,∠BAC=∠DAF=90°,
∵∠BAD=∠BAC﹣∠DAC,∠CAF=∠DAF﹣∠DAC,
∴∠BAD=∠CAF,
在△BAD与△CAF中,
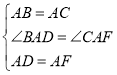 ,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,
延长BD,分别交直线AC、CF于点M,G,如图,
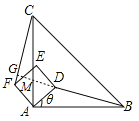
∵△BAD≌△CAF,
∴∠ABM=∠GCM,
∵∠BMA=∠CMG,
∴∠BGC=∠BAC=90°,
∴BD⊥CF.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目