题目内容
【题目】如图,AB=AC,CD∥AB,点E是AC上一点,且∠ABE=∠CAD,延长BE交AD于点F.
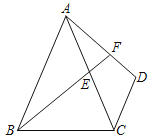
(1)求证:△ABE≌△CAD;
(2)如果∠ABC=65°,∠ABE=25°,求∠D的度数.
【答案】(1)见解析;(2)105°
【解析】
(1)根据ASA可证明△ABE≌△CAD;
(2)求出∠BAC=50°,则求出∠BAD=75°,可求出答案.
(1)证明:∵CD∥AB,
∴∠BAE=∠ACD,
∵∠ABE=∠CAD,AB=AC,
∴△ABE≌△CAD(ASA);
(2)解:∵AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣65°﹣65°=50°,
又∵∠ABE=∠CAD=25°,
∴∠BAD=∠BAC+∠CAD=50°+25°=75°,
∵AB∥CD,
∴∠D=180°﹣∠BAD=180°﹣75°=105°.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目