题目内容
【题目】某课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;
(3)当这个苗圃园的面积不小于100平方米时,直接写出x的取值范围.

【答案】(1)x=12;(2)最小值为:88平方米,最大值为:112.5平方米;(3) 6≤x≤10.
【解析】(1)根据题意得:(30﹣2x)x=72,解得:x=3,x=12,∵30﹣2x≤18,∴x=12;
(2)设苗圃园的面积为y,∴y=x(30﹣2x)=﹣2x2+30x,∵a=﹣2<0,∴苗圃园的面积y有最大值,∴当x=![]() 时,即平行于墙的一边长15>8米,y最大=112.5 平方米;
时,即平行于墙的一边长15>8米,y最大=112.5 平方米;
∵6≤x≤11,∴当x=11时,y最小=88平方米;
(3)由题意得:﹣2x2+30x≥100,∵30﹣2x≤18
解得:6≤x≤10.

练习册系列答案
相关题目
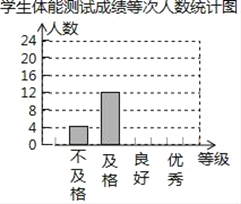
【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级,统计员在将测试数据绘制成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如图图表,请按正确数据解答下列各题:
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 | 8 |
|
良好 | 16 |
|
及格 | 12 |
|
不及格 | 4 |
|
合计 | 40 |
|
(1)填写统计表;
(2)根据调整后数据,补全条形统计图;
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.