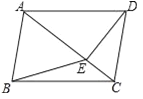
题目内容
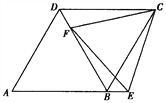
【题目】如图,以正方形ABCD的对角线BD为边作菱形BDEF,当点A,E,F在同一直线上时,∠F的正切值为___________.
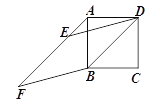
【答案】![]()
【解析】连接BD与AC相交于O,过点E作EG⊥BD于G,可得四边形AOEG是矩形,可得GE=AO,再根据直角三角形30°所对的直角边等于斜边的一半,求出∠EDG=30°即可求出答案.
证明:连接AC交BD于O,过点E作EG⊥BD于G;
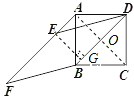
∵正方形ABCD
∴∠ACB=∠DBC=45°,AC=BD=2BO,∠BOC=90°,
∵菱形AEFC,∠F=∠DB,∠DEF=180°-∠F,
∴EF=BF,BD∥EF,
∴∠BAF=∠DBA=45°,
∴∠CAF=∠BAC+∠BAF=90°,
∵EG⊥BD,
∴四边形AOEG是矩形,
∴GE=AO,
∴DE=2GE,
∴∠EDG=30°,
∴∠F=30°
∴∠F的正切值为![]() .
.
“点睛”本题考查了正方形的性质,矩形的判定与性质,菱形的性质,直角三角形30°所对的直角边等于斜边的一半的性质,作辅助线构造出矩形的和30°的直角三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目