题目内容
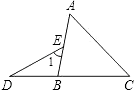
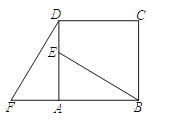
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若点E是AC的中点,判断BE与AC的位置关系,并说明理由;
(3)若△ABE是等边三角形,AD=![]() ,求对角线AC的长.
,求对角线AC的长.
【答案】(1)证明见解析;(2)BE⊥AC;(3)![]() .
.
【解析】
试题分析:(1)根据平行四边形的性质得出∠ABC+∠DCB=180°,推出∠ADC+∠BCD=180°,根据平行线的判定得出AD∥BC,根据平行四边形的判定推出即可;
(2)求出AD=DC,根据菱形的判定得出四边形ABCD是菱形,根据等腰三角形的性质得出即可;
(3)根据等边三角形的性质得出AB=AE,∠BAC=60°,求出∠DCE=∠BAE=60°,求出CD=2EC,设CE=x,则AB=DC=AE=2x,根据勾股定理得出方程,求出x,即可得出答案.
试题解析:(1)证明:∵AB∥CD,∴∠ABC+∠DCB=180°,∵∠ABC=∠ADC,∴∠ADC+∠BCD=180°,∴AD∥BC,∵AB∥CD,∴四边形ABCD是平行四边形;
(2)解:BE⊥AC,理由是:∵DE⊥AC,E为AC的中点,∴AD=DC,∵四边形ABCD是平行四边形,∴四边形ABCD是菱形,∴AB=BC,∵E为AC的中点,∴BE⊥AC;
(3)解:∵△ABE是等边三角形,∴AB=AE,∠BAC=60°,∵AB∥DC,∴∠DCE=∠BAE=60°,∵∠DEC=90°,∴∠CDE=30°,∴CD=2EC,设CE=x,则AB=DC=AE=2x,由勾股定理得:DE2=AD2﹣AE2=DC2﹣CE2,即![]() ,解得:x=
,解得:x=![]() (负数舍去),即CE=
(负数舍去),即CE=![]() ,AE=
,AE=![]() ,∴AC=
,∴AC=![]() .
.

练习册系列答案
相关题目