题目内容
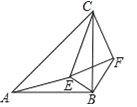
【题目】如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
(1)求证:△CAE∽△CBF.
(2)若BE=1,AE=2,求CE的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)首先由△ABC和△CEF均为等腰直角三角形可得AC:BC=CE:CF,∠ACE=∠BCF;然后根据相似三角形判定的方法,推得△CAE∽△CBF即可;
(2)首先根据△CAE∽△CBF,判断出∠CAE=∠△CBF,再根据∠CAE+∠CBE=90°,判断出∠EBF=90°;然后在Rt△BEF中,根据勾股定理,求出EF的长度,再根据CE、EF的关系,求出CE的长是多少即可.
试题解析:(1)证明:∵△ABC和△CEF均为等腰直角三角形,∴![]() =
=![]() ,∴∠ACB=∠ECF=45°,∴∠ACE=∠BCF,∴△CAE∽△CBF;
,∴∠ACB=∠ECF=45°,∴∠ACE=∠BCF,∴△CAE∽△CBF;
(2)解:∵△CAE∽△CBF,∴∠CAE=∠CBF,![]() =
=![]() ,又∵
,又∵![]() =
=![]() ,AE=2,∴
,AE=2,∴![]() =
=![]() ,∴BF=
,∴BF=![]() ,又∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,∴∠EBF=90°,∴
,又∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°,∴∠EBF=90°,∴![]() =
=![]() =3,∴EF=
=3,∴EF=![]() ,∵
,∵![]() =6,∴CE=
=6,∴CE=![]() .
.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目