题目内容
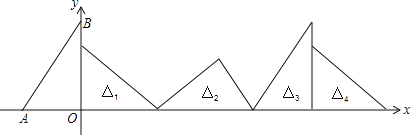
【题目】如图,在直角坐标系中,已知点A(-3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2016的直角顶点的坐标为 ( )
A. 8065 B. 8064 C. 8063 D. 8062
【答案】B
【解析】试题分析:先利用勾股定理计算出AB,从而得到△ABC的周长为12,根据旋转变换可得△OAB的旋转变换为每3次一个循环,由于2016=3×672,于是可判断三角形2016与三角形1的状态一样,然后计算672×12即可得到三角形2016的直角顶点坐标.
解:解:∵A(﹣3,0),B(0,4),
∴OA=3,OB=4,
∴AB=![]() =5,
=5,
∴△ABC的周长=3+4+5=12,
∵△OAB每连续3次后与原来的状态一样,
∵2016=3×672,
∴三角形2016与三角形1的状态一样,
∴三角形2016的直角顶点的横坐标=672×12=8064,
∴三角形2016的直角顶点坐标为(8064,0).
∴△2016的直角顶点的横坐标为8064
故选B.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案【题目】2017年李明家买了一辆轿车,他连续记录了一周中每天行驶的路程(如下表),以50km为标准,多于50km的记“+”,不足50km的记“-”,刚好506m的记“0”.
周一 | 周二 | 周三 | 周四 | 周五 | 周六 | 周日 | |
路程(km) | -6 | 0 | -12 | 7 | -9 | +15 | +12 |
(1)请你求出李明家轿车一周中平均每天行驶多少千米?
(2)如果每行驶100km需要汽油8升,汽油价格6.85元/升,请计算李明家轿车一个月(按30天计算)的汽油费是多少元(精确到个位)?
【题目】如图,一条街道旁有A,B,C,D,E五幢居民楼,某大桶水经销商统计各楼居民每周所需大桶水的数量如下表:
楼号 | A | B | C | D | E |
大桶水/桶 | 38 | 55 | 50 | 72 | 85 |
他计划在这五幢楼中租赁一间门市房,设立大桶水供应点,若仅考虑这五幢楼内的居民取水所走路程之和最小,则可以选择的地点应在( ).
![]()
A. B楼 B. C楼 C. D楼 D. E楼