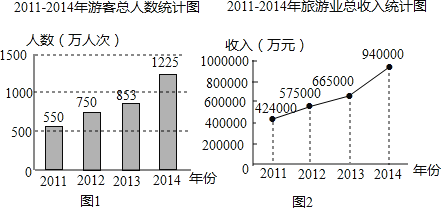
题目内容
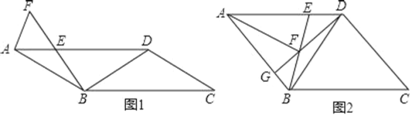
【题目】在ABCD中,连接对角线BD,AB=BD,E为线段AD上一点,AE=BE,F为射线BE上一点,DE=BF,连接AF.
(1)如图1,若∠BED=60°,CD=2![]() ,求EF的长;
,求EF的长;
(2)如图2,连接DF并延长交AB于点G,若AF=2DE,求证:DF=2GF.
【答案】(1)2;(2)见解析
【解析】
(1)先证明△BDE是直角三角形,解直角三角形求出BE,DE即可解决问题;
(2)作FH∥AB交AE于H.设DE=BF=a,则AF=2a.再证明AH=EH=DE=a,根据FH∥AB,EF=FB,推出![]() 即可.
即可.
(1)解:如图1中,
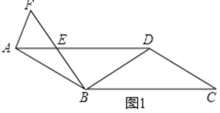
∵四边形ABCD是平行四边形,
∴AB=CD=![]() ,
,
∵AB=BD,
∴BD=![]()
∵EA=EB,
∴∠EAB=∠EBA,
∵∠DEB=60°,∠DEB=∠EAB+∠EBA,
∴∠BAD=∠EBA=∠ADB=30°,
∴∠EBD=90°,
∴BE=2,DE=2BE=4,
∵BF=DE,
∴BF=4,
∴EF=BF﹣BE=4﹣2=2.
(2)证明:作FH∥AB交AE于H.设DE=BF=a,则AF=2a.
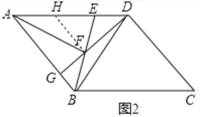
∵EA=EB,BA=BD,
∴∠EAB=∠EBA=∠ADB,
∵BF=DE,
∴△ABF≌△BDE(SAS),
∴BE=AF=2a,
∴EF=a,EA=EB=2a,
∵FH∥AB,EF=FB,
∴AH=EH=a,
∴![]() ,
,
∴DF=2FG.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目