题目内容
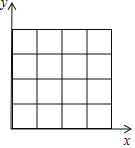
【题目】如图,在4×4的网格中,每一个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点,以O为坐标原点建立如图所示的平面直角坐标系.若抛物线y=x2+bx+c的图象至少经过图中(4×4的网格中)的三个格点,并且至少一个格点在x轴上,则符合要求的抛物线一定不经过的格点坐标为( )
A.(1,3)B.(2,3)C.(1,4)D.(2,4)
【答案】B
【解析】
二次项系数为1,该抛物线开口向上,根据二次函数的图象和性质进行若过(1,3),则可过点(2,0),此时抛物线解析式为:y=x2-6x+8,过另一个点(4,0),故A不符合题意;同理,可计算B,C,D选项中的格点是否符合题意.
解:∵二次项系数为1,
∴该抛物线开口向上
选项A:若过(1,3),则可过点(2,0),此时抛物线解析式为:y=x2-6x+8,过另一个点(4,0),故A不符合题意;
选项B:若过(2,3),则可过点(3,1),此时抛物线解析式为:y=x2﹣7x+13,若同时过x轴上的可能的格点(4,0),此时x=4时,y=1,故B符合题意;
选项C:若过(1,4),则可过点(3,0),此时抛物线解析式为:y=x2-6x+9,过另一个点(4,1),故C不符合题意;
选项D:若过(2,4),则可过点(4,0),此时抛物线解析式为:y=x2-8x+16,过另一个点(3,1),故D不符合题意;
故选:B.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目