��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y��kx+k��˫����y��![]() ��x��0�����ڵ�A��1��a����
��x��0�����ڵ�A��1��a����
��1����a��k��ֵ��
��2����ֱ֪��l����D��2��0����ƽ����ֱ��y��kx+k����P��m��n����m��3����ֱ��l��һ���㣬����P�ֱ���x�ᡢy���ƽ���ߣ���˫����y��![]() ��x��0���ڵ�M��N��˫�����ڵ�M��N֮��IJ������߶�PM��PN��Χ�ɵ��������߽磩��ΪW���ᡢ�����궼�������ĵ�������㣮
��x��0���ڵ�M��N��˫�����ڵ�M��N֮��IJ������߶�PM��PN��Χ�ɵ��������߽磩��ΪW���ᡢ�����궼�������ĵ�������㣮
�ٵ�m3 ʱ��ֱ��д������W �ڵ����������
��������W �������㣬�Ҹ��������� 5 �������ͼ���� m ��ȡֵ��Χ��
���𰸡���1��![]() ����2��0����3��
����2��0����3��![]() ��
��![]() ��
��
��������
��1������A��1��a�������������Ľ���ɵô𰸣�
��2������ƽ��![]() �ҹ�D��ֱ�߽���ʽ���������⻭��ͼ�Σ��۲��������ɵõ��٢ڵĴ𰸣�
�ҹ�D��ֱ�߽���ʽ���������⻭��ͼ�Σ��۲��������ɵõ��٢ڵĴ𰸣�
�⣺��1����A��1��a������![]() ��
��![]() ��
��
����A��1��4��������![]() ������
������![]() ����ã�
����ã�![]() ��
��
��2���١�ֱ��l����D��2��0����ƽ����ֱ��y=2x+2��
��ֱ��![]() �Ľ���ʽΪy=2x-4��
�Ľ���ʽΪy=2x-4��
��![]() ʱ��
ʱ��![]() ��
��
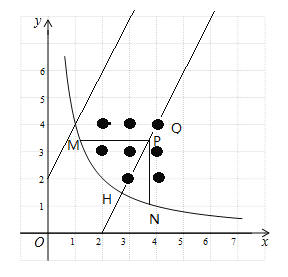
���P��������3��2����
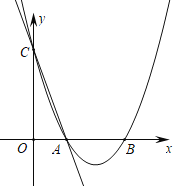
�������⻭��ͼ������ͼ��ʾ��
�۲�ͼ�Σ���֪������W�ڵ����������0��
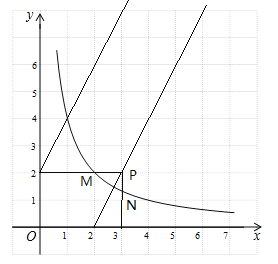
������ͼ��������W �������㣬�Ҹ���������5�������ͼ��ã�P���߶�QH�ϣ��Ҳ���H�غϣ���ͼ��֪��Q��4��4����
��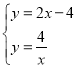 ��ã�
��ã�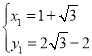 ��
��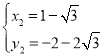
���ԣ�H![]()
���ԣ�![]() ��
��![]()
![]()
![]()

 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�