题目内容
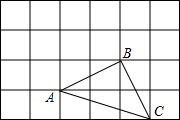
已知:如图,AB是⊙O的直径,弦CD交AB于E点,BE=1,AE=5,∠AEC=30°,求CD的长.


作OM⊥CD于点M,连接OC,则CM=
CD,
∵BE=1,AE=5,
∴OC=
AB=
=
=3,
∴OE=OB-BE=3-1=2,
∵Rt△OME中,∠AEC=30°,
∴OM=
OE=
×2=1,
在Rt△OCM中,
∵OC2=OM2+MC2,即32=12+CM2,解得CM=2
,
∴CD=2CM=2×2
=4
.
答:CD的长为4
.

| 1 |
| 2 |
∵BE=1,AE=5,
∴OC=
| 1 |
| 2 |
| BE+AE |
| 2 |
| 1+5 |
| 2 |
∴OE=OB-BE=3-1=2,
∵Rt△OME中,∠AEC=30°,
∴OM=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OCM中,
∵OC2=OM2+MC2,即32=12+CM2,解得CM=2
| 2 |
∴CD=2CM=2×2
| 2 |
| 2 |
答:CD的长为4
| 2 |


练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目