题目内容

【题目】△ABC在边长为l的正方形网格中如图所示．

①以点C为位似中心，作出△ABC的位似图形△A1B1C，使其位似比为1：2．且△A1B1C位于点C的异侧，并表示出A1的坐标．

②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C．

③在②的条件下求出点B经过的路径长．

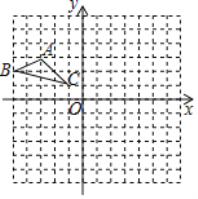
【答案】①作图见解析，点A1的坐标为（3，﹣3）；②作图见解析；③

【解析】

①延长AC到A1使A1C＝2AC，延长BC到B1使B1C＝2BC，则△A1B1C满足条件；

②利用网格特点和旋转的性质画出A、B的对应点A2、B2，从而得到△A2B2C．

③先计算出OB的长，然后根据弧长公式计算点B经过的路径长．

解：①如图，△A1B1C为所作，点A1的坐标为（3，﹣3）；

②如图，△A2B2C为所作；

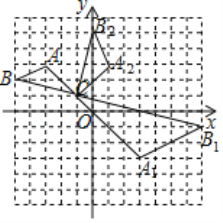
③，

点B经过的路径长．

练习册系列答案
相关题目

【题目】（1）问题发现：如图1，已知点为线段上一点，分别以线段为直角边作两个等腰直角三角形，，连接，线段之间的数量关系为__；位置关系为_________．

（2）拓展研究：如图2，把绕点C逆时针旋转，线段交于点F，则之间的关系是否仍然成立，说明理由；

（3）解决问题：如图3，已知，连接，把线段AB绕点A旋转，若，请直接写出线段的取值范围．

【题目】如图，已知一次函数y1＝ax＋b（a≠0）与反比例函数y2＝（k＞0），两函数图象交于(4，1)，(﹣2，n)两点．

（1）求a，k的值；

（2）若y2＞y1＞0，求x的取值范围．

【题目】如图，第一象限内的点A在反比例函数y＝上，第二象限的点B在反比例函数y＝上，且OA⊥OB，，BC、AD垂直于x轴于C、D，则k的值为_____．

【题目】2019年12月以来，湖北省武汉市部分医院陆续发现不明原因肺炎病例，现已证实该肺炎为一种新型冠状病毒感染的肺炎，其传染性较强.为了有效地避免交叉感染，需要采取以下防护措施：①戴口罩；②勤洗手；③少出门；④重隔离；⑤捂口鼻；⑥谨慎吃．某公司为了解员工对防护措施的了解程度（包括不了解、了解很少、基本了解和很了解），通过网上问卷调查的方式进行了随机抽样调查（每名员工必须且只能选择一项），并将调查结果绘制成如下两幅统计图．

请你根据上面的信息，解答下列问题

（1）本次共调查了_______名员工，条形统计图中________；

（2）若该公司共有员工1000名，请你估计不了解防护措施的人数；

（3）在调查中，发现有4名员工对防护措施很了解，其中有3名男员工、1名女员工.若准备从他们中随机抽取2名，让其在公司群内普及防护措施，求恰好抽中一男一女的概率．

【题目】在中，，，点是直线上一动点，点是直线上动点，点是直线上一动点，且，．

（1）如图1，当点，，分别在，，边上时，请你判断线段，，之间有怎样的数量关系？请直接写出你的结论；

（2）如图2，当在延长线上，在延长线上，在延长线上时，（1）中的结论是否成立？若成立，请利用图2证明；若不成立，请判断线段，，之间有怎样的数量关系？并证明你的结论；

（3）若，当时，请直接写出的长．

【题目】如图，抛物线y＝ax2+bx+3（a≠0）与x轴，y轴分别交于点A（﹣1，0），B（3，0），点C三点．

（1）求抛物线的解析式；

（2）x轴上是否存在点P，使PC+PB最小？若存在，请求出点P的坐标及PC+PB的最小值；若不存在，请说明理由；

（3）连接BC，设E为线段BC中点．若M是抛物线上一动点，将点M绕点E旋转180°得到点N，当以B、C、M、N为顶点的四边形是矩形时，直接写出点N的坐标．

【题目】如图，D是△ABC的边AB上一点，CE∥AB，DE交AC于点F，若FA=FC．

（1）求证：四边形ADCE是平行四边形；

（2）若AE⊥EC，EF=EC=5，求四边形ADCE的面积．

【题目】矩形ABCD中，AB=4，BC=8，折叠ABCD使点A与点C重合，折痕为EF，则EF的长为（ ）

A.B.C.D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网