题目内容
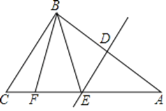
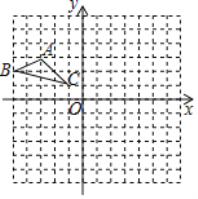
【题目】(1)问题发现:如图1,已知点![]() 为线段
为线段![]() 上一点,分别以线段
上一点,分别以线段![]() 为直角边作两个等腰直角三角形,
为直角边作两个等腰直角三角形,![]() ,连接
,连接![]() ,线段
,线段![]() 之间的数量关系为__;位置关系为_________.
之间的数量关系为__;位置关系为_________.
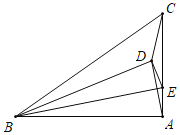
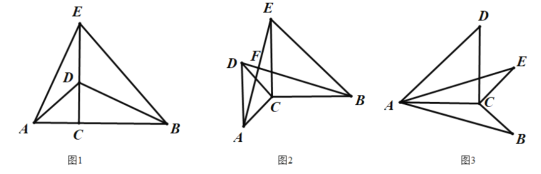
(2)拓展研究:如图2,把![]() 绕点C逆时针旋转,线段
绕点C逆时针旋转,线段![]() 交于点F,则
交于点F,则![]() 之间的关系是否仍然成立,说明理由;
之间的关系是否仍然成立,说明理由;
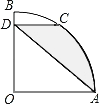
(3)解决问题:如图3,已知![]() ,连接
,连接![]() ,把线段AB绕点A旋转,若
,把线段AB绕点A旋转,若![]() ,请直接写出线段
,请直接写出线段![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)仍然成立,见解析;(3)
;(2)仍然成立,见解析;(3)![]()
【解析】
(1)根据题目条件证△ACE≌△DCB,再根据全等三角形的性质即可得出答案;
(2)依然用SAS证![]() ,根据全等三角形的性质即可证得;
,根据全等三角形的性质即可证得;
(3)连接BD,由(2)可知,AE=BD,在△ABD中,根据三角形三边关系即可求出AE的取值范围.
解:(1)![]() .
.
∵![]()
![]()
∴△ACE≌△DCB,
∴AE=BD,∠CAE=∠CDB
∴AE⊥BD;
(2)![]() 仍然成立.
仍然成立.
由题意得,∵△ACD和△BCE是等腰直角三角形
![]()
即![]() ,
,
∴![]()
∴![]() .
.
∴![]()
∴![]() .
.
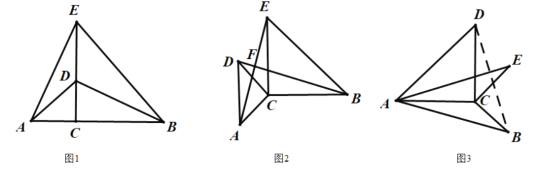
(3)![]()
连接BD.
由(2)可知,AE=BD,
在△ABD中,且![]() ,
,
所以![]()
即![]()
在AB绕点A旋转过程中,
当A,B,D三点在一条直线上时,![]() 或者
或者![]()
∴![]() ≤AE≤
≤AE≤![]()
如图所示.

【题目】为了解某校初二学生每周上网的时间,两位学生进行了抽样调查.小丽调查了初二电脑爱好者中40名学生每周上网的时间;小杰从全校400名初二学生中随机抽取了40名学生,调查了每周上网的时间.小丽与小杰整理各自样本数据,如下表所示:
时间段 (小时/周) | 小丽抽样 人数 | 小杰抽样 人数 |
0~1 | 6 | 22 |
1~2 | 10 | 10 |
2~3 | 16 | 6 |
3~4 | 8 | 2 |
(每组可含最低值,不含最高值)
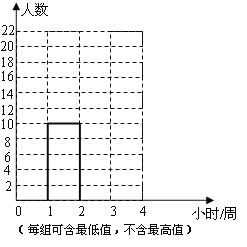
(1)你认为哪位同学抽取的样本不合理?请说明理由;
(2)根据合理抽取的样本,把上图中的频数分布直方图补画完整;
(3)专家建议每周上网2小时以上(含2小时)的同学应适当减少上网的时间,估计该校全体初二学生中有多少名同学应适当减少上网的时间?