题目内容
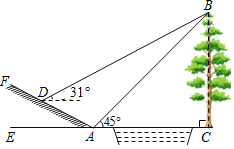
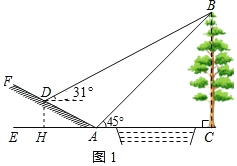
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
【答案】(1)小明从点A到点D的过程中,他上升的高度为3米;(2)大树的高度约为16.5米.
【解析】
(1)作DH⊥AE于H,解Rt△ADH,即可求出DH;
(2)延长BD交AE于点G,解Rt△GDH、Rt△ADH,求出GH、AH,得到AG;设BC=x米,根据正切的概念用x表示出GC、AC,根据GC﹣AC=AG列出方程,解方程得到答案.
(1)作DH⊥AE于H,如图1所示:
在Rt△ADH中,∵![]() ,∴AH=2DH.
,∴AH=2DH.
∵AH2+DH2=AD2,∴(2DH)2+DH2=(3![]() )2,∴DH=3.
)2,∴DH=3.
答:小明从点A到点D的过程中,他上升的高度为3米;
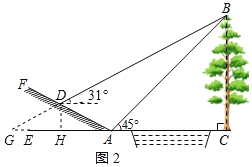
(2)如图2所示:延长BD交AE于点G,设BC=xm,由题意得:∠G=31°,∴GH![]() 5.
5.
∵AH=2DH=6,∴GA=GH+AH=5+6=11.
在Rt△BGC中,tan∠G![]() ,∴CG
,∴CG![]() x.
x.
在Rt△BAC中,∠BAC=45°,∴AC=BC=x.
∵GC﹣AC=AG,∴![]() x﹣x=11,解得:x=16.5.
x﹣x=11,解得:x=16.5.
答:大树的高度约为:16.5米.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目