题目内容
【题目】已知,等边△ABC,点 E 在 BA 的延长线上,点 D 在 BC 上,且 ED=EC.
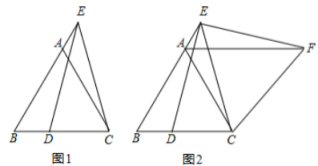
(1)如图 1,求证:AE=DB;
(2)如图 2,将△BCE 绕点 C 顺时针旋转 60°至△ACF(点 B、E 的对应点分别为点 A、F),连接 EF.在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对线段长度之差等于 AB 的长.
【答案】(1)见解析;(2)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
(1)在BA上截取BF=BD,连接DF,根据等边三角形的性质可得∠BAC=∠B=∠ACB=60°,从而证出△BDF为等边三角形,然后利用AAS证出△CEA≌△EDF,从而得出AE=DF,即可证出结论;
(2)根据图形、全等三角形的性质、旋转的性质和等量代换即可得出结论.
解:(1)在BA上截取BF=BD,连接DF
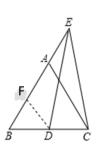
∵△ABC是等边三角形
∴∠BAC=∠B=∠ACB=60°,
∵BF=BD,
∴△BDF为等边三角形
∴BD=DF,∠BFD=∠FDB=60°
∴∠BFD=∠BAC
∴FD∥AC
∴∠EAC=∠DFE
∵ED=EC
∴∠EDC=∠ECD
∵∠EDC+∠EDF=180°-∠FDB=120°,∠ECD+∠CEA=180°-∠B=120°
∴∠CEA=∠EDF
在△CEA和△EDF中
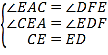
∴△CEA≌△EDF
∴AE=DF
∴AE=DB
(2)由图可知:![]()
∵AE=DB
∴![]()
由旋转的性质可得:BE=AF
∴![]()
∴![]()

练习册系列答案
相关题目